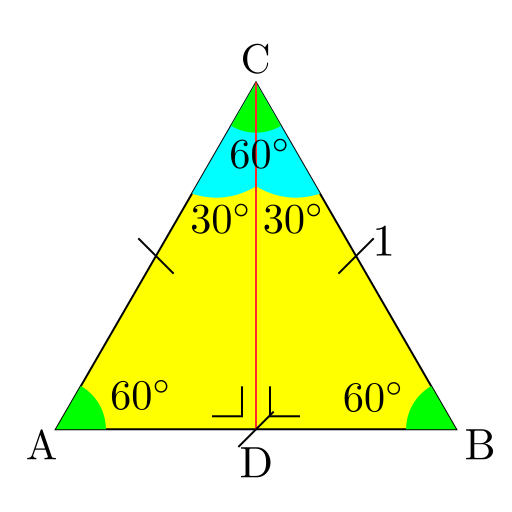
# Dengan Segitiga Sama Sisi

Menggunakan keistimewaan segitiga sama sisi yang semua sudutnya $60\degree$.

Misalkan kita mempunyai segitiga sama sisi dengan panjang sisi 1. Kemudian kita buat garis tinggi dari $c$ sehingga segitiga terbelah menjadi 2 segitiga siku-siku. Karena sudut $\angle CAD=60\degree$ maka sudut $\angle ACD=90\degree - 60\degree = 30 \degree$. Karena sudut $\angle CBD=60\degree$ maka sudut $\angle BCD=90\degree - 60\degree = 30 \degree$.

Karena kedua segitiga siku-siku mempunyai sudut internal sama, berbagi satu garis sebagai sisi dan salah satu sisi mempunyai panjang sama maka kedua segitiga adalah kongruen. Jadi sisi didepan sudut $30\degree$ pada segitiga ACD (yaitu AD) dan BCD (yaitu BD) sama panjang ($AD = BD$). Maka berlaku:

$$\begin{aligned} AB &= AD + BD \\ &= 2AD \\ AD &= \frac{1}{2}AB \\ &= \frac{1}{2} \times 1 \\ &= \frac{1}{2} \end{aligned}$$

Kita sekarang bisa mencari panjang $CD$

$$\begin{aligned} AD^2 + CD^2 &= AC^2 \\ CD^2 &= AC^2 - AD^2 \\ &= (AC - AD)(AC + AD) \\ &= (1 - \frac{1}{2})(1 + \frac{1}{2}) \\ &= \frac{1}{2}\times \frac{3}{4} \\ &= \frac{3}{4} \\ CD &= \sqrt{\frac{3}{4}} \\ &= \frac{\sqrt{3}}{2} \end{aligned}$$

Jadi kita bisa mengetahui nilai trigonometri:

$$\begin{aligned} \sin(\angle ACD) &= \sin(30 \degree) \\ &= \frac{AD}{AC} \\ &= \frac{(\frac{1}{2})}{1} \\ &= \frac{1}{2} \\ \cos(\angle ACD) &= \cos(30 \degree) \\ &= \frac{CD}{AC} \\ &= \frac{(\frac{\sqrt{3}}{2})}{1} \\ &= \frac{\sqrt{3}}{2} \\ \tan(\angle ACD) &= \tan(30 \degree) \\ &= \frac{AD}{CD} \\ &= \frac{(\frac{1}{2})}{\frac{(\sqrt{3}}{2})} \\ &= \frac{1}{2}\times \frac{2}{\sqrt{3}} \\ &= \frac{1}{\sqrt{3}}\times \frac{\sqrt{3}}{\sqrt{3}} \\ &= \frac{\sqrt{3}}{3} \\ \sin(\angle CAD) &= \sin(60 \degree) \\ &= \frac{CD}{AC} \\ &= \frac{\sqrt{3}}{2} \\ \cos(\angle CAD) &= \cos(60 \degree) \\ &= \frac{AD}{AC} \\ &= \frac{1}{2} \\ \tan(\angle CAD) &= \tan(60 \degree) \\ &= \frac{CD}{AD} \\ &= \frac{(\frac{\sqrt{3}}{2})}{(\frac{1}{2})} \\ &= \frac{\sqrt{3}}{2}\times \frac{2}{1} \\ &= \sqrt{3} \\ \end{aligned}$$

# Kesimpulan

Nilai fungsi trigonometri sudut $30\degree$ dan $60\degree$

$$\begin{align*} \sin(30 \degree) &= \dfrac{1}{2} \\ \cos(30 \degree) &= \dfrac{\sqrt{3}}{2} \\ \tan(30 \degree) &= \dfrac{\sqrt{3}}{3} \\ \sin(60 \degree) &= \dfrac{\sqrt{3}}{2} \\ \cos(60 \degree) &= \dfrac{1}{2} \\ \tan(60 \degree) &= \sqrt{3} \end{align*}$$