Grafik fungsi sin, cos dan tan akan terus berulang-ulang bahkan ke arah kiri (x negatif) sehingga disebut fungsi sinusoidal/periodic

# Fitur Fungsi Sinusoidal/Periodic

Fungsi periodik mempunyai 3 fitur yaitu:

• Garis tengah (midline)
  Garis horizontal yang membagi grafik menjadi dua bagian yang sama panjang. Atau garis yang berada di tengah antara nilai maksimum dan minimum.
• Amplitudo (amplitude)
  Jarak vertikal antara titik extremum (minimum dan maksimum) dengan garis tengah.
• Periode
  Jarak horizontal antara dua titik minimum. Atau jarak horizontal dua titik maksimum. Atau jarak horizontal yang dibutuhkan untuk membuat satu gunung satu lembah (tidak harus berurutan). Atau 2 kali jarak horizontal antara titik yang menyinggung garis tengah (nilai keempatnya sama)

# Fungsi Normal (y = sin(x), y = cos(x), y = tan(x))

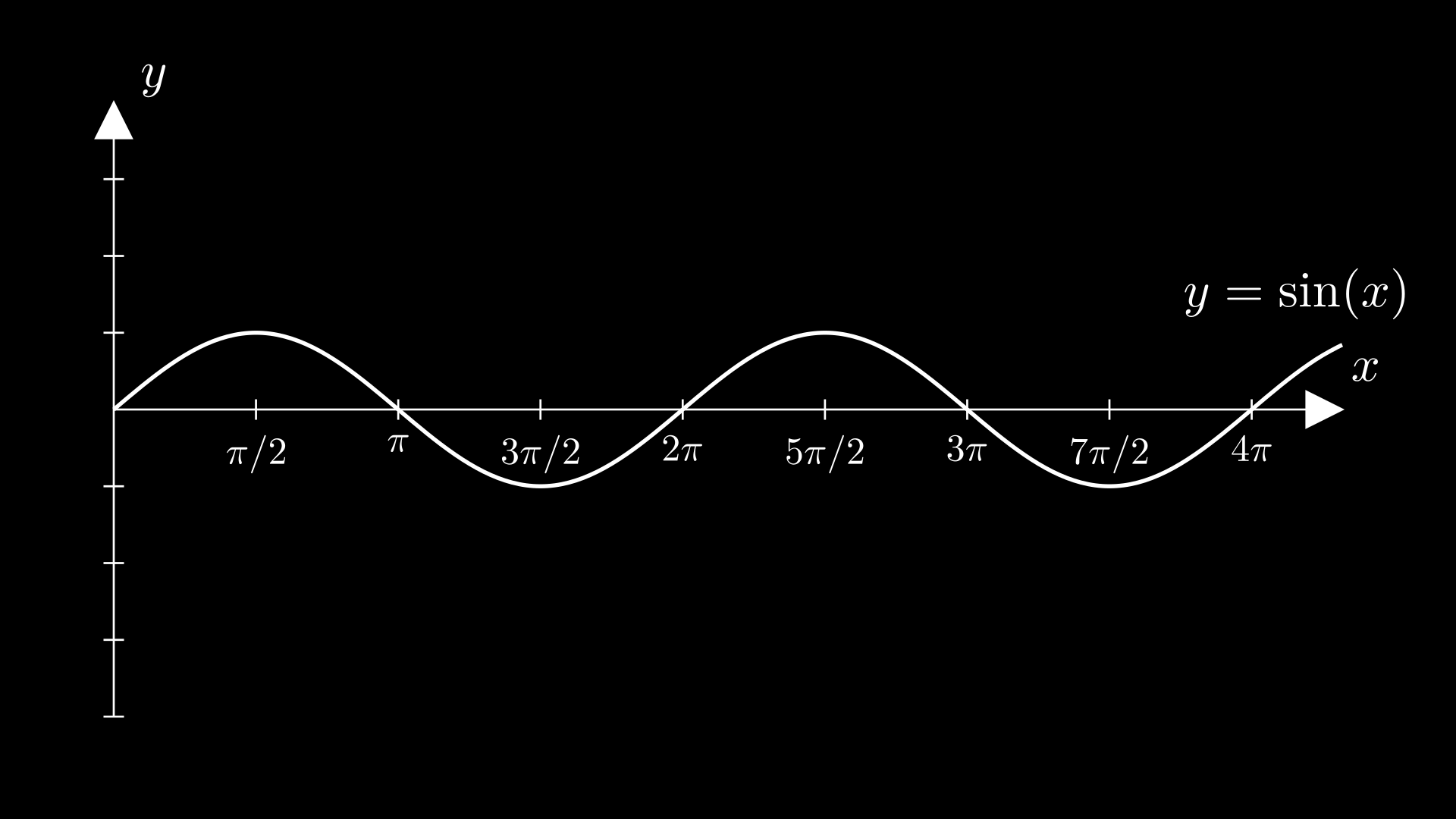
Grafik fungsi sinus tersebut akan berulang-ulang.

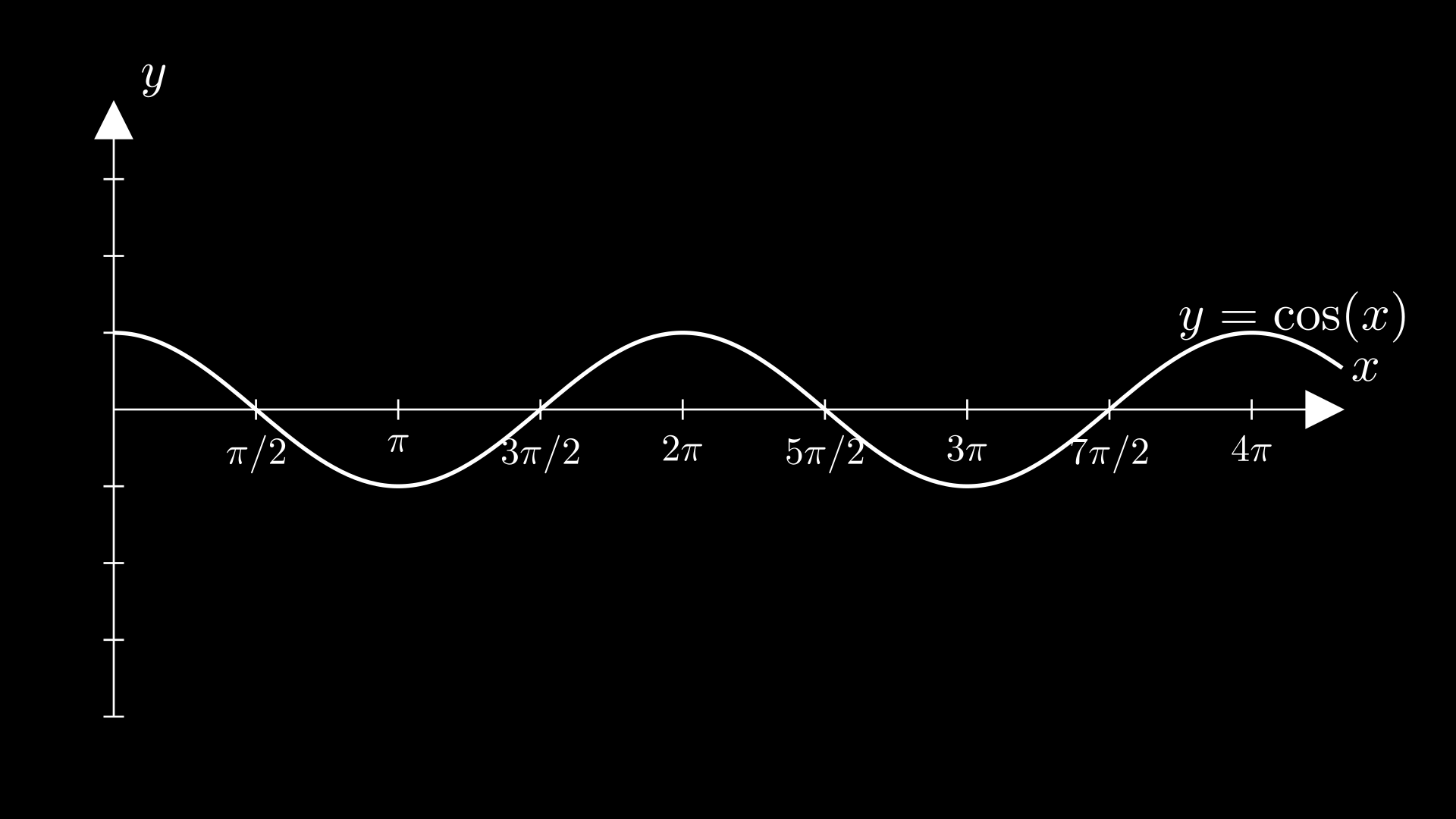
Grafik sin dan cos mirip, bedanya adalah grafik sin dimulai dengan satu gunung penuh dan grafik cos dimulai dengan setengah gunung

Dalam fungsi sin normal dan cos normal, nilai maksimumnya adalah 1, nilai minimumnya -1, nilai tengahnya 0, dan amplitudonya 1. Karena fungsi berulang saat $2\pi$ maka periodenya $2\pi$ .

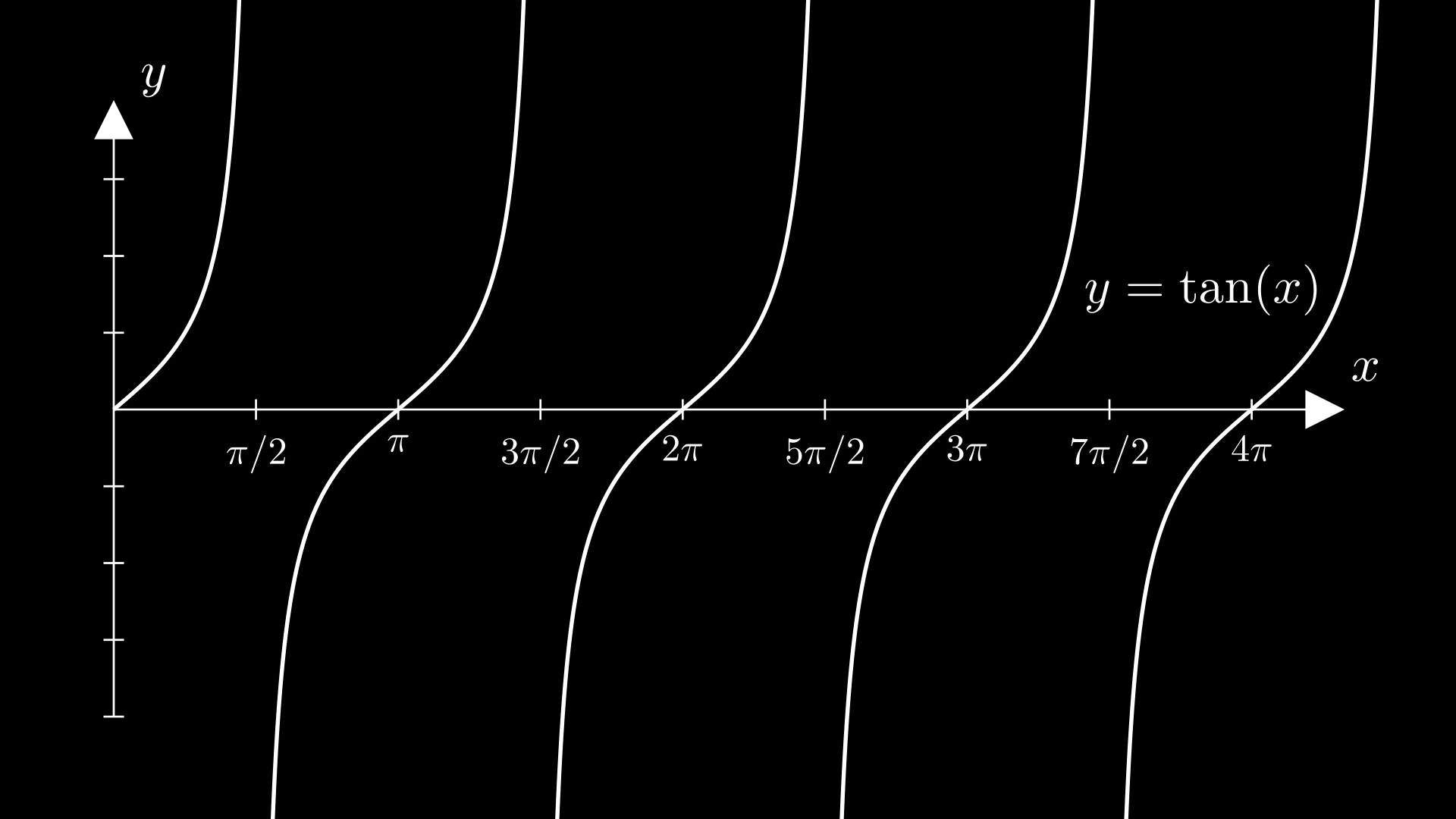
Dalam fungsi tan normal, nilai maksimum = $\infty$, minimum = $-\infty$. Nilai tengahnya 0 dan amplitudonya $\infty$. Karena fungsi berulang pertama kali saat $\pi$ maka periodenya = $\pi$

# Fungsi y = a sin/cos(x)

Nilai maksimum terjadi saat nilai sin/cos bernilai maksimum yaitu 1. Jadi nilai maksimumnya:

$$\begin{align*} |a|(\sin/\cos(x))| &= |a|\times1 \\ &= |a| \end{align*}$$

Perlu menggunakan nilai mutlak, karena jika $a$ negatif nilai maksimum fungsi terjadi saat nilai sin/cos minimum dan seterusnya

Nilai minimum terjadi saat nilai sin/cos bernilai minimum yaitu -1. Jadi nilai minimumnya:

$$\begin{align*} |a|(\sin/\cos(x)) &= |a|\times-1 \\ &= -|a| \end{align*}$$

Nilai tengah terjadi saat nilai sin/cos bernilai nilai tengahnya yaitu 0. Jadi nilai tengahnya:

$$\begin{align*} a(\sin/\cos(x)) &= a\times0 \\ &= 0 \end{align*}$$

Maka amplitudonya:

$$\begin{align*} \text{nilai maksimum} - \text{nilai tengah} &= |a| - 0 \\ &= |a| \end{align*}$$

Jika $a$ negatif, maka terjadi refleksi terhadap garis tengah.

# Fungsi y = sin/cos(x) + a

Nilai tengah fungsi:

$$\begin{align*} (\sin/\cos(x)) + a &= 0 + a\\ &= a \end{align*}$$

Nilai maksimum fungsi:

$$\begin{align*} |(\sin/\cos(x)) + a| &= 1 + a\\ &= a + 1 \end{align*}$$

Nilai maksimum sin/cos = 1, maka nilai maksimum fungsi = $1 + a$.

Nilai minimum sin/cos = -1, maka nilai minimum fungsi = $-1 + a$.

# Fungsi y = sin/cos(ax)

1 gunung dan 1 lembah pertama kali terbentuk saat input fungsi sin/cos bernilai $2\pi$. Maka:

$$\begin{align*} ax & =2\pi\\ x & =\frac{2\pi}{a} \end{align*}$$

Nilai $x$ menentukan kapan 1 gunung dan 1 lembah pertama kali terbentuk. Karena 1 gunung dan 1 lembah pertama mempunyai awal di $x=0$. Maka periodenya:

$$|\dfrac{2\pi}{a}-0|=\frac{2\pi}{|a|}$$

Saat $a$ negatif, grafiknya terbalik.

# Fungsi y = sin/cos(x + a)

Grafik fungsi akan bergeser. Awal dari grafik sin/cos terjadi saat masukannya bernilai 0. Jadi awal grafik sin/cos pada fungsi adalah:

$$\begin{align*} x+a & =0\\ x & =-a \end{align*}$$

Nilai $x$ kapan grafik fungsi sin/cos dimulai. Dengan kata lain, grafik bergeser sebesar $-a$.

# Fungsi y = a sin/cos(bx + c) + d

Nilai tengah fungsi:

$$\begin{align*} a(\sin/\cos) + d &= a\times 0 + d \\ &= d \end{align*}$$

Nilai maksimum fungsi:

$$\begin{align*} |a|(\sin/\cos) + d &= |a|\times 1 + d \\ &= |a| + d \end{align*}$$

Nilai minimum fungsi:

$$\begin{align*} |a(\sin/\cos)| + d &= |a|\times -1 + d \\ &= -|a| + d \end{align*}$$

Amplitudo:

$$\begin{align*} \text{nilai maksimum} - \text{nilai tengah} &= |a| + d - d \\ &= |a| \\ &\text{atau}\\ \text{nilai tengah} - \text{nilai minimum} &= d - (-|a| + d) \\ &= d + |a| - d \\ &= |a| \end{align*}$$

Nilai $x$ saat argument sin/cos = 0:

$$\begin{align*} bx + c &= 0 \\ x &= \frac{-c}{b} \end{align*}$$

Jadi grafik bergeser sebesar $\dfrac{-c}{b}$.

Nilai $x$ saat argument sin/cos = $2\pi$

$$\begin{align*} bx + c &= 2\pi \\ x &= \frac{2\pi - c}{b} \end{align*}$$

Karena awal grafik bergeser, maka periodenya:

$$\begin{align*} |\frac{2\pi-c}{b}-\left(\frac{-c}{b}\right)| & =|\frac{2\pi-c+c}{b}|\\ & =|\frac{2\pi}{b}|\\ & =\frac{2\pi}{|b|} \end{align*}$$

Untuk membuat fungsi sin/cos dari grafik, dapat menggunakan sifat di atas. Terutama garis tengah, periode dan amplitudo.