Grafik yang membentuk parabola

Bentuk:

$$y = ax^2 + bx + c$$

Dengan $a \neq 0$, $x, y \in \Re$ dan $a, b, c \in \Re$

# Titik Potong

# Titik Potong dengan Sumbu X

Memotong sumbu x berarti $y = 0$, berarti

$$0 = ax^2 + bx + c$$

Titik potongya adalah penyelesaian dari persamaan tersebut. Koordinatnya $(x_1, 0)$ dan $(x_2,0 )$

# Titik Potong dengan Sumbu Y

Memotong sumbu y berarti $x = 0$. Jadi

$$\begin{aligned} f(x) &= ax^2 + bx + c \\ f(0) &= a \cdot 0^2 + b \cdot 0 + c \\ f(0) &= c \end{aligned}$$

Maka koordinatnya adalah $(0, c)$

# Titik Puncak Parabola

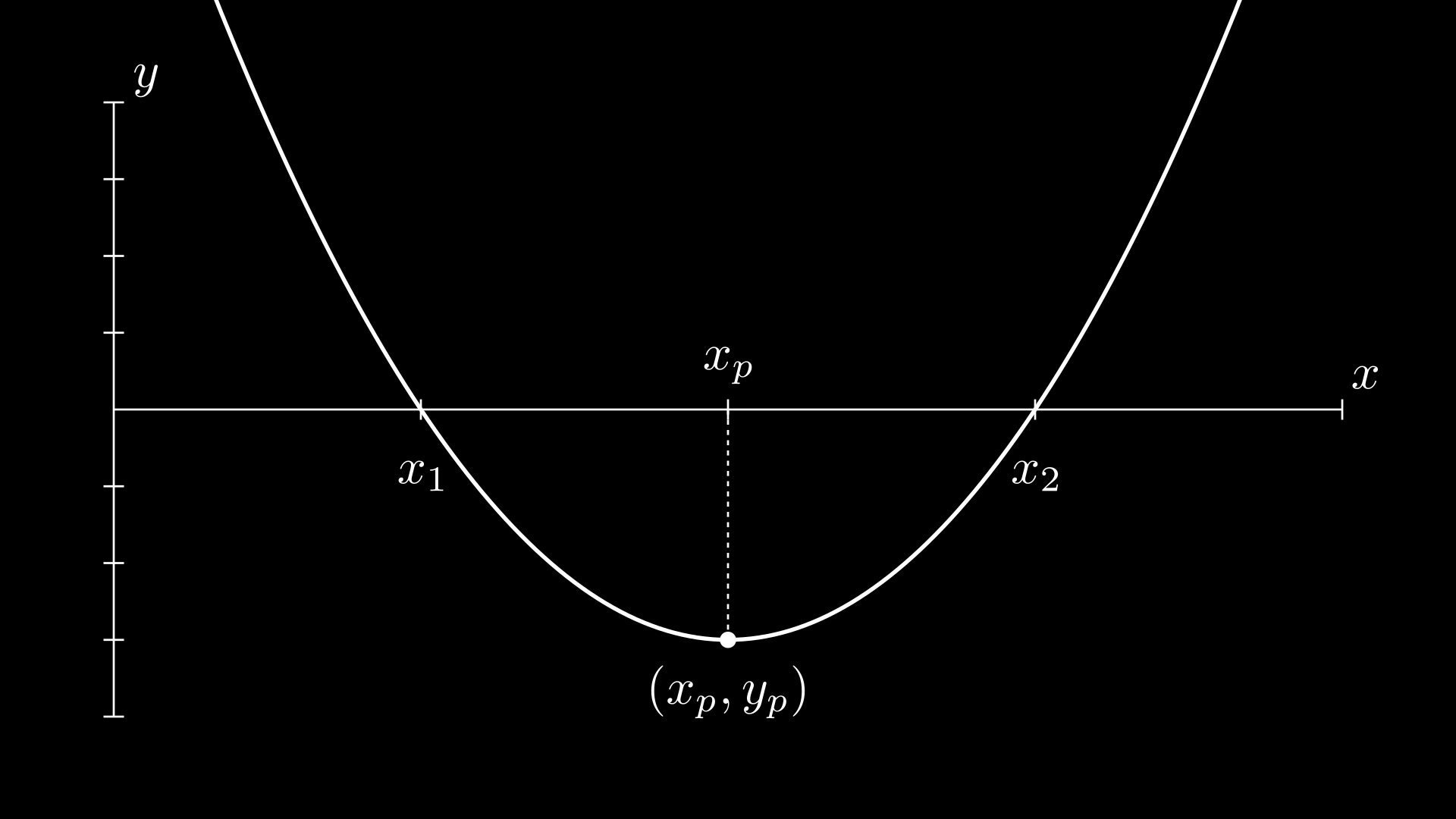
Nilai x pada titik puncak jelas berada di tengah-tengah antara dua titik perpotongan dengan sumbu x. Misalkan $x_2 > x_1$. Maka titik puncak rumusnya:

$$\begin{aligned}x & =x_{1}+\frac{x_{2}-x_{1}}{2}\\ & =\frac{2x_{1}}{2}+\frac{x_{2}-x_{1}}{2}\\ & =\frac{x_{1}+x_{2}}{2}\\ & =\frac{\left(\dfrac{-b}{a}\right)}{2}\\ & =\frac{-b}{2a} \end{aligned}$$

Nilai x ini juga disebut dengan sumbu simetri. Karena jika dijadikan garis vertikal akan membelah/membagi grafik menjadi dua bagian yang sama (simetri).

Nilai y dapat dicari dengan memasukkan nilai x pada persamaan.

$$\begin{aligned} y & =f( x)\\ f( x) & =ax^{2} +bx+c\\ f\left(\frac{-b}{2a}\right) & =a\left(\frac{-b}{2a}\right)^{2} +b\left(\frac{-b}{2a}\right) +c\\ & =\frac{ab^{2}}{4a^{2}} +\frac{-b^{2}}{2a} +c\\ & =\frac{ab^{2}}{4a^{2}} +\frac{-2ab^{2}}{4a^{2}} +\frac{4a^{2} c}{4a^{2}}\\ & =\frac{ab^{2} -2ab^{2} +4a^{2} c}{4a^{2}}\\ & =\frac{-ab^{2} +4a^{2} c}{4a^{2}} \times \frac{a}{a}\\ & =\frac{-b^{2} +4ac}{4a} \times \frac{-1}{-1}\\ & =\frac{b^{2} -4ac}{4a}\\ & =\frac{D}{-4a} \end{aligned}$$

Nilai y juga disebut nilai ekstrim karena merupakan nilai maksimum/minimum dari fungsi kuadrat. Jadi koordinat titik puncak adalah $(\frac{-b}{2a}, f\left(\frac{-b}{2a}\right))$ atau $(\frac{-b}{2a}, \frac{D}{-4a})$

# Sifat-sifat

# Berdasarkan nilai a

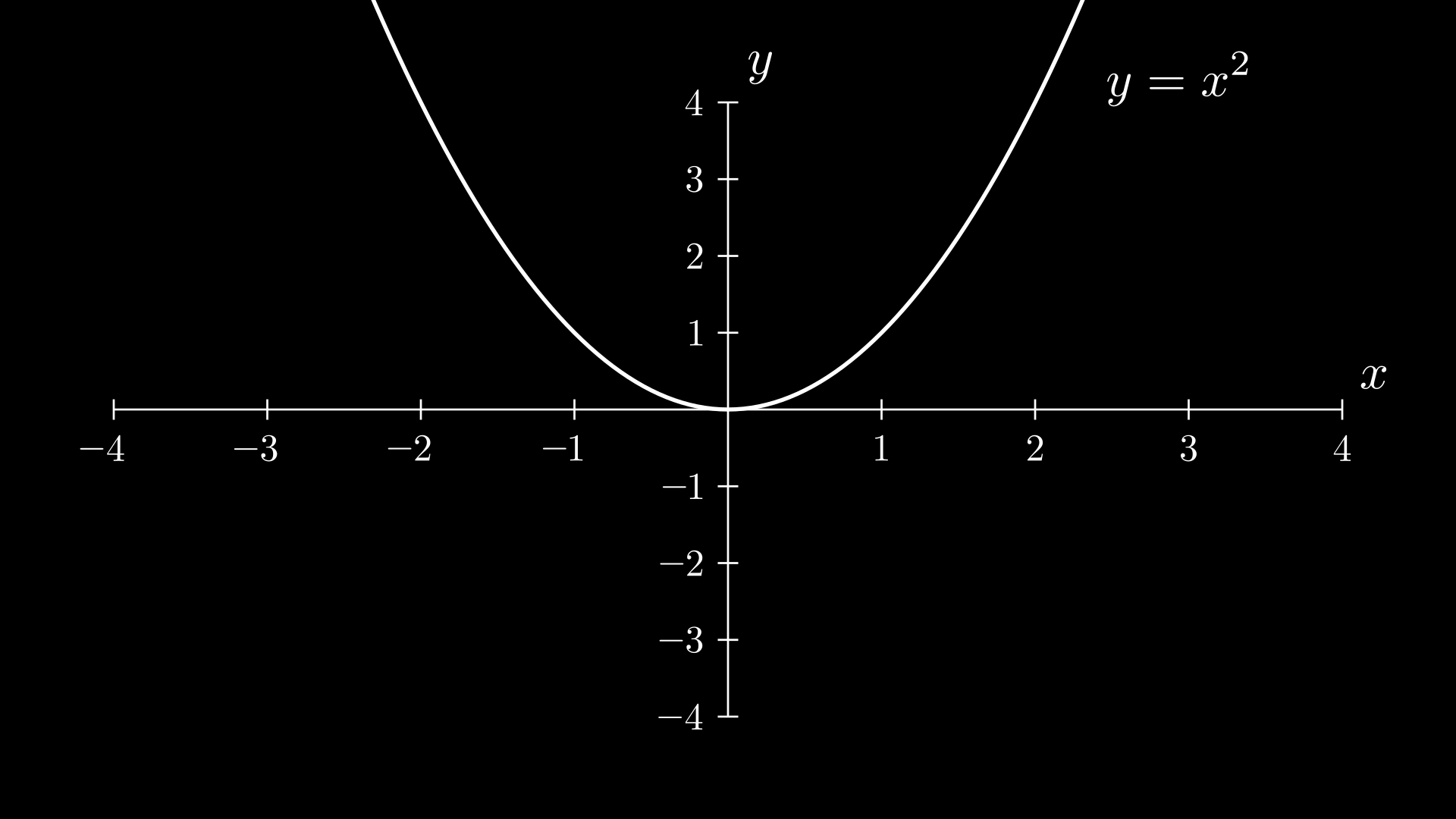
1. $a > 0$, grafik membuka ke atas (parabola)
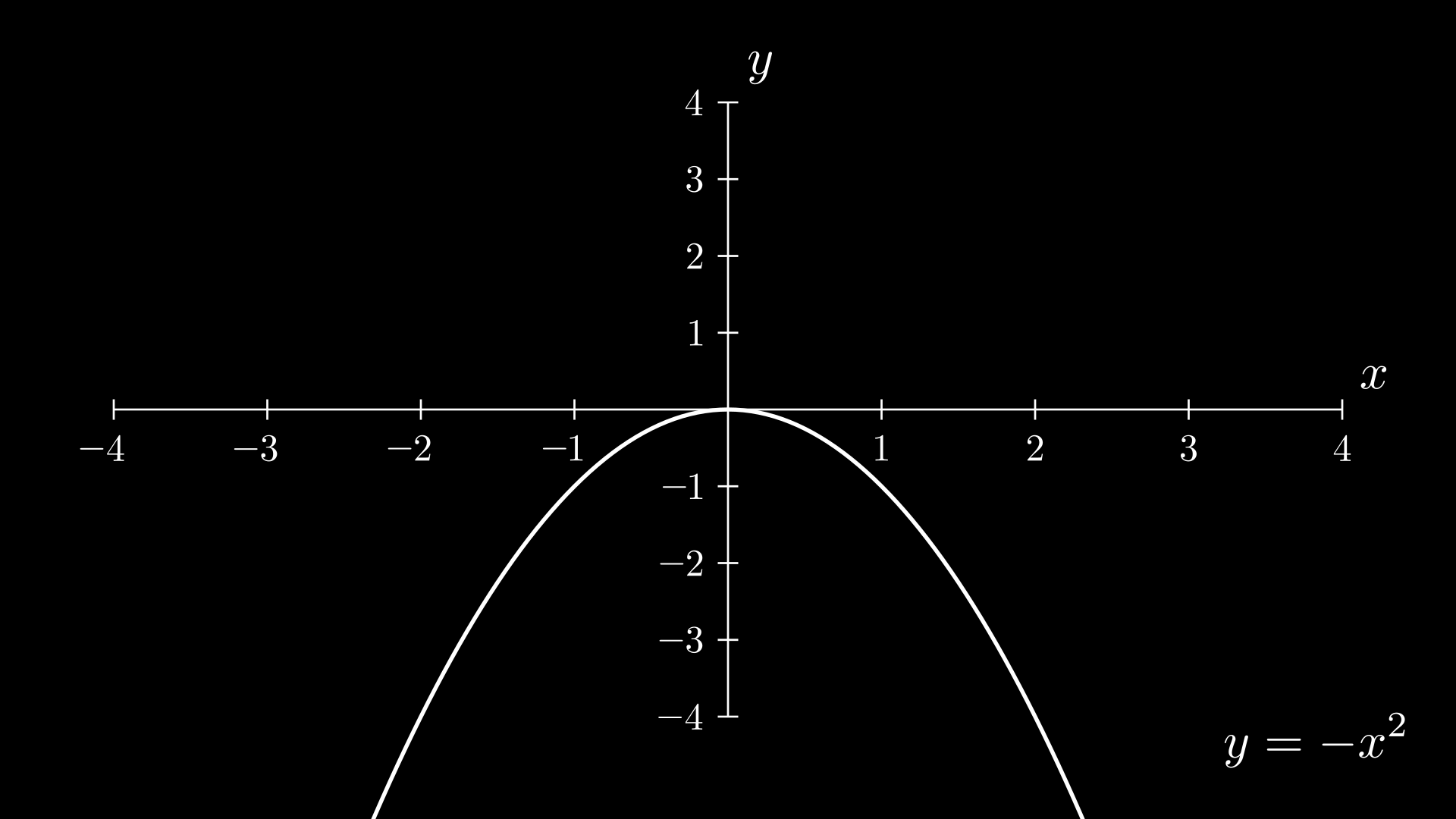
2. $a < 0$, grafik membuka ke bawah (parabola terbalik)

Pembuktian: Dapat dibuktukan dengan menganalisa nilai y saat x = 0, 1 dan -1

$$\begin{aligned} f(x) &= x^2 \\ f(0) &= 0 \\ f(1) &= 1 \\ f(-1) &= -1 \\ \end{aligned}$$

$$\begin{aligned} f(x) &= -x^2 \\ f(0) &= 0 \\ f(1) &= -1 \\ f(-1) &= 1 \\ \end{aligned}$$

# Berdasarkan nilai D/Diskriminan

Perpotongan dengan sumbu X ditentukan oleh akar-akar dari fungsi. Jadi, berlaku sifat-sifat diskriminan pada perpotongan dengan sumbu x. Sifatnya adalah:

1. $D > 0$, memotong sumbu x di 2 titik
2. $D = 0$, memotong sumbu x di 1 titik
3. $D < 0$, tidak memotong sumbu x

# Berdasarkan nilai c

Nilai $c$ menentukan koordinat y saat memotong sumbu y. Jadi

1. $c > 0$, memotong sumbu y di atas sumbu x
2. $c = 0$, memotong sumbu y si sumbu x
3. $c < 0$, memotong sumbu y di bawah sumbu x

# Berdasarkan nilai a dan b

1. $a > 0$ dan $b > 0$ atau $a < 0$ dan $b < 0$, titik puncak di kiri sumbu y
2. $b = 0$, titik puncak di sumbu y
3. $a > 0$ dan $b < 0$ atau $a < 0$ dan $b > 0$, titik puncak di kanan sumbu y

Pembuktian:

Saat $a > 0$ dan $b > 0$

$$x = \frac{-b}{2a} = \frac{- \cdot +}{+} = -$$

Saat $a < 0$ dan $b < 0$

$$x = \frac{-b}{2a} = \frac{- \cdot -}{-} = - \cdot + = -$$

Saat $b = 0$

$$x = \frac{-b}{2a} = \frac{0}{2a} = 0$$

Saat $a > 0$ dan $b < 0$

$$x = \frac{-b}{2a} = \frac{- \cdot -}{+} = - \cdot - = +$$

Saat $a < 0$ dan $b > 0$

$$x = \frac{-b}{2a} = \frac{- \cdot +}{-} = - \cdot - = +$$

# Berdasarkan nilai a dan D

1. $a > 0$ dan $D > 0$ atau $a < 0$ dan $D < 0$, titik puncak di bawah sumbu x
2. $D = 0$, titik puncak di sumbu x
3. $a < 0$ dan $D > 0$ atau $a > 0$ dan $D < 0$, titik puncak di atas sumbu y

Pembuktian

Saat $a > 0$ dan $D > 0$

$$y = \frac{D}{-4a} = \frac{+}{- \cdot +} = \frac{+}{-} = -$$

Saat $a < 0$ dan $D < 0$

$$y = \frac{D}{-4a} = \frac{-}{- \cdot -} = \frac{-}{+} = -$$

Saat $D = 0$

$$y = \frac{D}{-4a} = \frac{0}{-4a} = 0$$

Saat $a < 0$ dan $D > 0$

$$y = \frac{D}{-4a} = \frac{+}{- \cdot -} = \frac{+}{+} = +$$

Saat $a > 0$ dan $D < 0$

$$y = \frac{D}{-4a} = \frac{-}{- \cdot +} = \frac{-}{-} = +$$

# Menyusun Grafik Fungsi Kuadrat

# Jika Melewati Sumbu X pada 2 Titik dan Melewati Suatu Titik

Hampir sama dengan menyusun persamaan kuadrat jika diketahui akar-akarnya. Rumusnya

$$y = a(x - x_1)(x - x_2)$$

Bedanya ada $a$. Perbedaan itu terjadi karena:

Misal kita membuat persamaan kuadrat dengan akar -1 dan 1.

$$\begin{align*} (x+1)(x-1) &= 0 \\ x^2 - 1 &= 0 \tag{1} \end{align*}$$

Kalikan persamaan tersebut dengan -1 dan 2.

$$\begin{align*} -x^2 + 1 &= 0 \tag{2} \end{align*}$$

$$\begin{align*} 2x^2 - 2 &= 0 \tag{3} \end{align*}$$

Persamaan 1,2 dan 3 mempunyai akar-akar yang sama. Lalu kita coba ubah persamaan tersebut menjadi fungsi kuadrat.

$$\begin{align*} f(x) = x^2 - 1 \tag{1} \end{align*}$$

$$\begin{align*} f(x) = -x^2 + 1 \tag{2} \end{align*}$$

$$\begin{align*} f(x) = 2x^2 - 2 \tag{3} \end{align*}$$

Jika dihitung ketiga fungsi memotong sumbu X pada titik yang sama. Lalu kita coba hitung nilai y saat $x = 2$

$$\begin{align*} y = 2^2 - 1 = 3 \tag{1} \end{align*}$$

$$\begin{align*} y = -2^2 + 1 = -3 \tag{2} \end{align*}$$

$$\begin{align*} f(x) = 2\cdot 2 ^2 - 2 = 3 \tag{3} \end{align*}$$

Kedua fungsi menghasilkan nilai yang berbeda. Namun perbedaanya teratur. Fungsi 2 berasal dari persamaan 2 dan persamaan 2 berasal dari persamaan 1 dikali -1. Ternyata nilai y fungsi 2 merupakan nilai y fungsi 1 dikali -1. Sehingga dibutuhkan $a$, agar bisa menghasilkan fungsi yang melewati suatu titik. Bisa dikatakan beberapa fungsi kuadrat berbeda dapat memotong sumbu Y pada koordinat yang sama, tetapi tidak dapat melewati titik-titik yang sama.

Nilai $a$ dapat dicari dengan memasukkan titik ke dalam rumus.

Hal ini terjadi karena perbedaan bentuk persamaan kuadrat dan fungsi kuadrat.

$$\begin{align*} ax^2 + bx + c = \boxed{0} & \text{\quad\textbar}\times 2\text{\textbar\quad} & 2ax^2 + 2bx + 2c = \boxed{0} \\ ax^2 + bx + c = \boxed{y} & \text{\quad\textbar}\times 2\text{\textbar\quad} & 2ax^2 + 2bx + 2c = \boxed{2y} \end{align*}$$

# Jika Memotong Sumbu X pada 1 Titik dan Melewati Suatu Titik

Berarti mempunyai dua akar yang sama:

$$\begin{align*} y &= a(x - x_1)(x - x_1) &= a(x - x_1)^2 \end{align*}$$

# Jika Diketahui Titik Puncaknya dan Melewati Suatu Titik

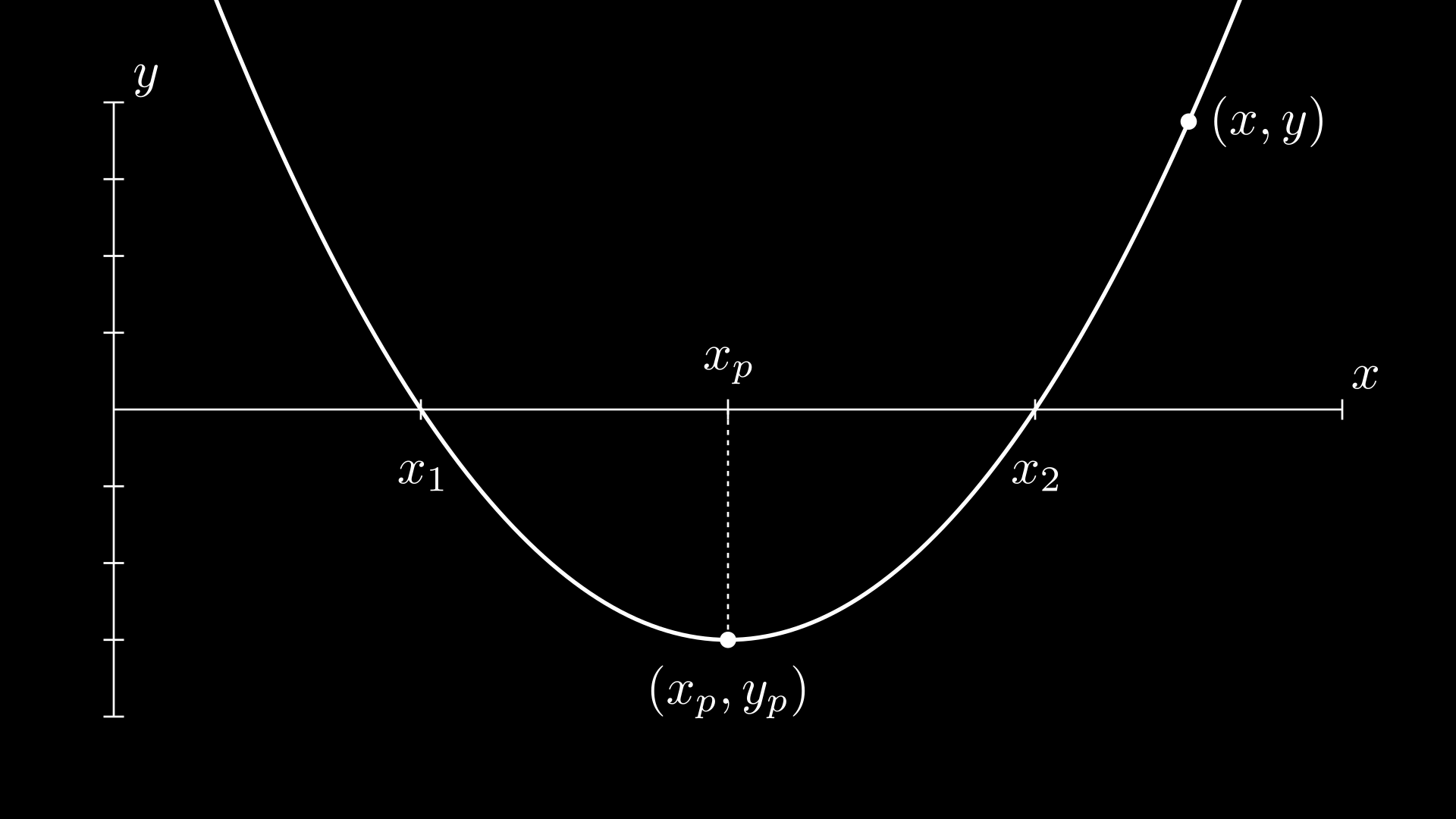
Dengan mencari hubungan titik puncak dan titik yang dilewati.

Persamaan untuk mencari titik puncak

$$\begin{align*} x_{p} & =\frac{x_{1}+x_{2}}{2}\\ 2x_{p} & =x_{1}+x_{2} \end{align*}$$

Fungsi kuadrat pada sembarang titik.

$$\begin{aligned}y & =a(x-x_{1})(x-x_{2})\\ & =a(x^{2}-x_{2}x-x_{1}x+x_{1}x_{2})\\ & =a(x^{2}-(x_{1}+x_{2})x+x_{1}x_{2})\\ & =a(x^{2}-2x_px+x_{1}x_{2}) \end{aligned}$$

Fungsi kudrat pada titik puncak.

$$\begin{aligned}y_{p} & =a(x_{p}-x_{1})(x_{p}-x_{2})\\ & =a(x_{p}^{2}-x_{2}x_{p}-x_{1}x_{p}+x_{1}x_{2})\\ & =a(x_{p}^{2}-(x_{1}+x_{2})x_{p}+x_{1}x_{2})\\ & =a(x_{p}^{2}-2x_{p}x_{p}+x_{1}x_{2})\\ & =a(x_{p}^{2}-2x_{p}^{2}+x_{1}x_{2})\\ & =a(-x_{p}^{2}+x_{1}x_{2}) \end{aligned}$$

Kurangkan kedua fungsi tadi

$$\begin{aligned}y-y_{p} & =a(x^{2}-2x_{p}x+x_{1}x_{2})-a(-x_{p}^{2}+x_{1}x_{2})\\ & =a(x^{2}-2x_{p}x+x_{1}x_{2}-(-x_{p}^{2}+x_{1}x_{2}))\\ & =a(x^{2}-2x_{p}x+x_{1}x_{2}+x_{p}^{2}-x_{1}x_{2}))\\ & =a(x^{2}-2x_{p}x+x_{p}^{2}))\\ y-y_{p} & =a(x-x_{p})^{2}\\ y & =a(x-x_{p})^{2}+y_{p} \end{aligned}$$

# Jika Diketahui Titik-Titik Lainnya

Buat beberapa persamaan dari titik-titik yang diketahui dengan memasukkannya pada rumus

$$y = ax^2 + bx + c$$

Carilah nilai $a$, $b$, dan $c$ dari persamaan yang telah dibuat. Masukkan nilai $a$, $b$, dan $c$ ke persamaan di atas. Persamaan baru adalah jawabannya