Derivatif merupakan operasi yang dipelajari di Kalkulus Diferensial yang merupakan cabang kalkulus.
Derivatif menunjukkan tingkat perubahan (cepat lambatnya) keluaran suatu fungsi saat masukannya
berubah.
Misalkan kita mempunyai fungsi s ( t ) s(t) s ( t ) t t t
s ( t ) = t 2 s(t) = t^2
s ( t ) = t 2
Saat t t t s ( t ) s(t) s ( t ) t = 2 t = 2 t = 2
v = Δ s Δ t = s 2 − s 1 t 2 − t 1 \begin{align*}
v &= \frac{\Delta s}{\Delta t} \\
&= \frac{s_2 - s_1}{t_2 - t_1}
\end{align*}
v = Δ t Δ s = t 2 − t 1 s 2 − s 1
Kita membutuhkan dua sampel jarak pada dua waktu yang berbeda untuk mengetahui kecepatan. Misalkan
sampel pertama kita ambil pada detik ke-2. Maka waktu dan jarak sampel ke 1 adalah:
t 1 = t = 2 s 1 = s ( t ) = s ( 2 ) \begin{align*}
t_1 &= t &&= 2 \\
s_1 &= s(t) &&= s(2)
\end{align*}
t 1 s 1 = t = s ( t ) = 2 = s ( 2 )
Lalu dari mana sampel ke-2?. Bagaimana jika sampel kedua kita ambil pada detik ke-0?. Ini tidak bisa
dilakukan. Kenapa?. Jika sampel ke-2 kita ambil pada detik ke-0, maka yang kita dapatkan adalah
kecepatan rata-rata dari detik ke-0 sampai detik ke-2.
Jika sampel kedua kita ambil pada waktu yang jauh dari detik ke-2, maka kita akan mendapatkan
kecepatan rata-rata dan hasilnya akan berbeda dengan kecepatan pada detik ke-2.
Bagaimana jika kita mengambil sampel kedua dari waktu yang dekat dengan waktu sampel pertama (detik
ke-2). Misalkan detik ke-2.1, ini akan memberikan kecepatan rata-rata tetapi karena perbedaan
waktunya cukup kecil maka ini bisa dianggap kecepatan sekitar detik ke-2.
Misal perbedaan waktu antara sampel pertama dan kedua adalah h h h
t 2 − t 1 = h t 2 = 2 + h s 2 = s ( 2 + h ) \begin{align*}
t_2 - t_1 &= h \\
t_2 &= 2 +h \\
s_2 &= s(2 + h)
\end{align*}
t 2 − t 1 t 2 s 2 = h = 2 + h = s ( 2 + h )
Maka persamaan untuk kecepatan dapat ditulis ulang menjadi:
v = s ( 2 + h ) − s ( 2 ) ( 2 + h ) − 2 = s ( 2 + h ) − s ( 2 ) h \begin{align*}
v &= \frac{s(2 + h) - s(2)}{(2 + h) - 2} \\
&= \frac{s(2 + h) - s(2)}{h}
\end{align*}
v = ( 2 + h ) − 2 s ( 2 + h ) − s ( 2 ) = h s ( 2 + h ) − s ( 2 )
Persamaan tersebut akan memberikan kecepatan sekitar detik ke-2. Jika perbedaan waktunya terlalu
kecil dan sampai bisa diabaikan maka persamaan tersebut akan memberikan kecepatan tepat detik ke-2.
Jadi makin kecil h h h v v v
Mari kita coba nilai h = 1 h = 1 h = 1
v = s ( 2 + h ) − s ( 2 ) h = s ( 2 + 1 ) − s ( 2 ) 1 = s ( 3 ) − s ( 2 ) 1 = 3 2 − 1 2 = 9 − 4 = 5 \begin{align*}
v & =\frac{s(2+h)-s(2)}{h}\\
& =\frac{s(2+1)-s(2)}{1}\\
& =\frac{s(3)-s(2)}{1}\\
& =3^{2}-1^{2}\\
& =9-4\\
& =5
\end{align*}
v = h s ( 2 + h ) − s ( 2 ) = 1 s ( 2 + 1 ) − s ( 2 ) = 1 s ( 3 ) − s ( 2 ) = 3 2 − 1 2 = 9 − 4 = 5
Kita coba lagi dengan memperkecil h h h
v = s ( 2.1 ) − s ( 2 ) 0.1 = 2. 1 2 − 1 2 0.1 = 4.41 − 4 0.1 = 0.41 0.1 = 4.1 \begin{align*}
v & =\frac{s(2.1)-s(2)}{0.1}\\
& =\frac{2.1^{2}-1^{2}}{0.1}\\
& =\frac{4.41-4}{0.1}\\
& =\frac{0.41}{0.1}\\
& =4.1
\end{align*}
v = 0.1 s ( 2.1 ) − s ( 2 ) = 0.1 2. 1 2 − 1 2 = 0.1 4.41 − 4 = 0.1 0.41 = 4.1
Kemudian coba lagi dengan h = 0.01 h = 0.01 h = 0.01
v = s ( 2.01 ) − s ( 2 ) 0.01 = 2.0 1 2 − 1 2 0.01 = 4.0401 − 4 0.01 = 0.0401 0.01 = 4.01 \begin{align*}
v & =\frac{s(2.01)-s(2)}{0.01}\\
& =\frac{2.01^{2}-1^{2}}{0.01}\\
& =\frac{4.0401-4}{0.01}\\
& =\frac{0.0401}{0.01}\\
& =4.01
\end{align*}
v = 0.01 s ( 2.01 ) − s ( 2 ) = 0.01 2.0 1 2 − 1 2 = 0.01 4.0401 − 4 = 0.01 0.0401 = 4.01
Kemudian coba lagi dengan h = 0.001 h = 0.001 h = 0.001
v = s ( 2.001 ) − s ( 2 ) 0.001 = 2.00 1 2 − 1 2 0.001 = 4.004001 − 4 0.001 = 0.004001 0.001 = 4.001 \begin{align*}
v & =\frac{s(2.001)-s(2)}{0.001}\\
& =\frac{2.001^{2}-1^{2}}{0.001}\\
& =\frac{4.004001-4}{0.001}\\
& =\frac{0.004001}{0.001}\\
& =4.001
\end{align*}
v = 0.001 s ( 2.001 ) − s ( 2 ) = 0.001 2.00 1 2 − 1 2 = 0.001 4.004001 − 4 = 0.001 0.004001 = 4.001
Kemudian kita coba lagi dengan h = 0.0001 h = 0.0001 h = 0.0001
v = s ( 2.0001 ) − s ( 2 ) 0.0001 = 2.000 1 2 − 1 2 0.0001 = 4.00040001 − 4 0.0001 = 0.00040001 0.0001 = 4.0001 \begin{align*}
v & =\frac{s(2.0001)-s(2)}{0.0001}\\
& =\frac{2.0001^{2}-1^{2}}{0.0001}\\
& =\frac{4.00040001-4}{0.0001}\\
& =\frac{0.00040001}{0.0001}\\
& =4.0001
\end{align*}
v = 0.0001 s ( 2.0001 ) − s ( 2 ) = 0.0001 2.000 1 2 − 1 2 = 0.0001 4.00040001 − 4 = 0.0001 0.00040001 = 4.0001
Jika dicoba h h h v v v h h h v v v v v v
v = lim h → 0 s ( 2 + h ) − s ( 2 ) h = lim h → 0 ( 2 + h ) 2 − 2 2 h = lim h → 0 2 2 + 4 h + h 2 − 2 2 h = lim h → 0 4 h + h 2 h = lim h → 0 4 h h + h 2 h = lim h → 0 4 + h = 4 \begin{align*}
v & =\lim_{h\to0}\frac{s(2+h)-s(2)}{h}\\
& =\lim_{h\to0}\frac{(2+h)^{2}-2^{2}}{h}\\
& =\lim_{h\to0}\frac{2^{2}+4h+h^{2}-2^{2}}{h}\\
& =\lim_{h\to0}\frac{4h+h^{2}}{h}\\
& =\lim_{h\to0}\frac{4h}{h}+\frac{h^{2}}{h}\\
& =\lim_{h\to0}4+h\\
& =4
\end{align*}
v = h → 0 lim h s ( 2 + h ) − s ( 2 ) = h → 0 lim h ( 2 + h ) 2 − 2 2 = h → 0 lim h 2 2 + 4 h + h 2 − 2 2 = h → 0 lim h 4 h + h 2 = h → 0 lim h 4 h + h h 2 = h → 0 lim 4 + h = 4
Bisa dikatakan kecepatan benda saat detik ke 2 adalah 4 (v = 4 v = 4 v = 4 v = 0 v = 0 v = 0
v v v s s s t t t v v v s s s t t t v v v
v = d s d t = lim h → 0 s ( t + h ) − s ( h ) h v = \frac{ds}{dt} = \lim_{h \to 0} \frac{s(t + h) - s(h)}{h}
v = d t d s = h → 0 lim h s ( t + h ) − s ( h )
d s d t \dfrac{ds}{dt} d t d s s s s t t t
Secara umum bisa dituliskan derivatif fungsi f f f x x x
d f d x = lim x → 0 f ( x + h ) − f ( h ) h \frac{df}{dx} = \lim_{x \to 0} \frac{f(x+h) - f(h)}{h}
d x df = x → 0 lim h f ( x + h ) − f ( h )
Derivatif adalah perbandingan antara perubahan keluaran suatu fungsi dengan perubahan masukan
fungsi tersebut dan perubahan masukan mendekati 0.
Kita bisa menggambar fungsi f ( x ) = x 2 f(x) = x^2 f ( x ) = x 2
y = f ( x ) d f d x = lim x → 0 f ( x + h ) − f ( h ) h \begin{align*}
y &= f(x) \\
\frac{df}{dx} &= \lim_{x \to 0} \frac{f(x+h) - f(h)}{h}
\end{align*}
y d x df = f ( x ) = x → 0 lim h f ( x + h ) − f ( h )
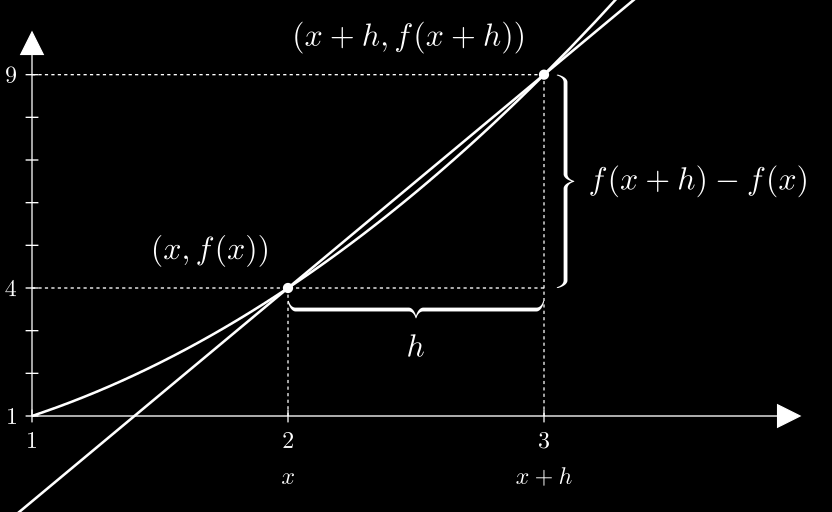
Pertama kita abaikan lim x → 0 \lim_{x \to 0} lim x → 0 x = 2 x = 2 x = 2 h = 1 h = 1 h = 1 x + h = 3 x+h=3 x + h = 3
Bisa dilihat bahwa
f ( x + h ) − f ( x ) h = perubahan y perubahan x \frac{f(x + h) - f(x)}{h} = \frac{\text{perubahan y}}{\text{perubahan x}}
h f ( x + h ) − f ( x ) = perubahan x perubahan y
Kita tahu bahwa perbandingan perubahan y y y x x x ( x , f ( x ) ) (x, f(x)) ( x , f ( x )) ( x + h , f ( x + h ) ) (x+h, f(x+h)) ( x + h , f ( x + h ))
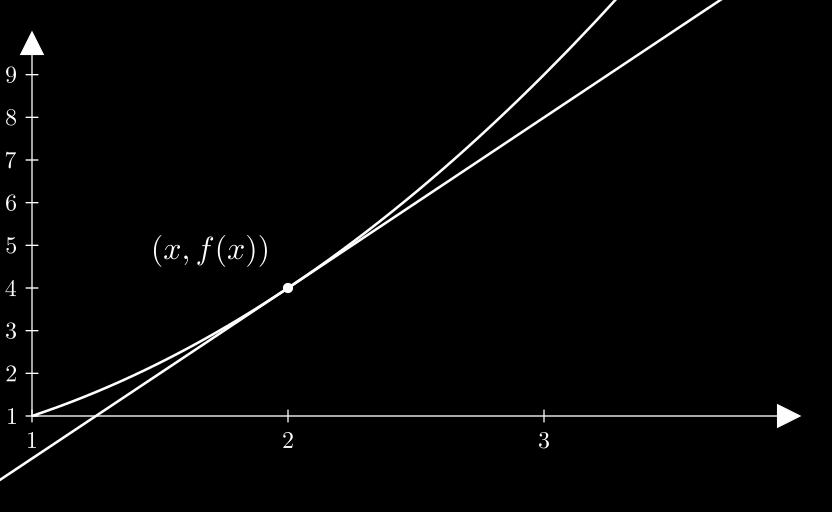
Sekarang kita terapkan lim h → 0 \lim_{h \to 0} lim h → 0
Saat h h h d f d x \dfrac{df}{dx} d x df
Derivasi menunjukkan kemiringan garis singgung yang menyinggung kurva fungsi pada titik tertentu.
Derivasi dari Konstanta
Misalkan fungsi f ( x ) = 5 f(x)=5 f ( x ) = 5 d f d x = 0 \frac{df}{dx}=0 d x df = 0
Bukti dengan menggunakan limit.
Misalkan c c c
f ( x ) = c d f d x = lim h → 0 f ( x + h ) − f ( x ) h = lim h → 0 c − c h = lim h → 0 0 h = 0 \begin{align*}
f(x) & =c\\
\frac{df}{dx} & =\lim_{h\to0}\frac{f(x+h)-f(x)}{h}\\
& =\lim_{h\to0}\frac{c-c}{h}\\
& =\lim_{h\to0}\frac{0}{h}\\
& =0
\end{align*}
f ( x ) d x df = c = h → 0 lim h f ( x + h ) − f ( x ) = h → 0 lim h c − c = h → 0 lim h 0 = 0
Derivasi dari konstanta adalah 0. Misal c c c d ( c ) d x = 0 \dfrac{d(c)}{dx}=0 d x d ( c ) = 0
Derivasi dari x
Fungsi y = x y=x y = x d ( x ) d x = 1 \dfrac{d(x)}{dx}=1 d x d ( x ) = 1
Bukti dengan limit:
d ( x ) d x = lim h → 0 f ( x + h ) − f ( x ) h = lim h → 0 x + h − x h = lim h → 0 h h = lim h → 0 1 = 1 \begin{align*}
\frac{d(x)}{dx} & =\lim_{h\to0}\frac{f(x+h)-f(x)}{h}\\
& =\lim_{h\to0}\frac{x+h-x}{h}\\
& =\lim_{h\to0}\frac{h}{h}\\
& =\lim_{h\to0}1\\
& =1
\end{align*}
d x d ( x ) = h → 0 lim h f ( x + h ) − f ( x ) = h → 0 lim h x + h − x = h → 0 lim h h = h → 0 lim 1 = 1
Derivasi dari x x x d ( x ) d x = 1 \dfrac{d(x)}{dx}=1 d x d ( x ) = 1
Aturan Pangkat
Ada pola tertentu saat kita mencari derivasi dari x n x^n x n
d ( x n ) d x = lim h → 0 ( x + h ) n − x n h \frac{d(x^n)}{dx} = \lim_{h\to 0} \frac{(x+h)^n - x^n}{h}
d x d ( x n ) = h → 0 lim h ( x + h ) n − x n
Menurut teorema binomial:
( x + h ) n = ∑ k = 0 n ( n k ) x n − k h k = ( n 0 ) x n h 0 + ( n 1 ) x n − 1 h 1 + ( n 2 ) x n − 2 h 2 + ( n 3 ) x 3 h 3 + … + ( n n ) x n − n h n = x n + ( n 1 ) x n − 1 h 1 + ( n 2 ) x n − 2 h 2 + ( n 3 ) x 3 h 3 + … + h n \begin{align*}
(x+h)^{n} & =\sum_{k=0}^{n}\binom{n}{k}x^{n-k}h^{k}\\
& =\binom{n}{0}x^{n}h^{0}+\binom{n}{1}x^{n-1}h^{1}+\binom{n}{2}x^{n-2}h^{2}+\binom{n}{3}x^{3}h^{3}+\ldots+\binom{n}{n}x^{n-n}h^{n}\\
& =x^{n}+\binom{n}{1}x^{n-1}h^{1}+\binom{n}{2}x^{n-2}h^{2}+\binom{n}{3}x^{3}h^{3}+\ldots+h^{n}
\end{align*}
( x + h ) n = k = 0 ∑ n ( k n ) x n − k h k = ( 0 n ) x n h 0 + ( 1 n ) x n − 1 h 1 + ( 2 n ) x n − 2 h 2 + ( 3 n ) x 3 h 3 + … + ( n n ) x n − n h n = x n + ( 1 n ) x n − 1 h 1 + ( 2 n ) x n − 2 h 2 + ( 3 n ) x 3 h 3 + … + h n
Maka:
d ( x n ) d x = lim h → 0 ( x + h ) n − x n h = lim h → 0 x n + ( n 1 ) x n − 1 h 1 + ( n 2 ) x n − 2 h 2 + ( n 3 ) x 3 h 3 + … + h n − x n h = lim h → 0 ( n 1 ) x n − 1 h 1 + ( n 2 ) x n − 2 h 2 + ( n 3 ) x 3 h 3 + … + h n h = lim h → 0 ( n 1 ) x n − 1 + ( n 2 ) x n − 2 h 1 + ( n 3 ) x 3 h 2 + … + h n − 1 = ( n 1 ) x n − 1 = n ! ( n − 1 ) ! 1 ! x n − 1 = n ( n − 1 ) ! ( n − 1 ) ! x n − 1 = n x n − 1 \begin{align*}
\frac{d(x^{n})}{dx} & =\lim_{h\to0}\frac{(x+h)^{n}-x^{n}}{h}\\
& =\lim_{h\to0}\frac{\cancel{x^{n}}+\binom{n}{1}x^{n-1}h^{1}+\binom{n}{2}x^{n-2}h^{2}+\binom{n}{3}x^{3}h^{3}+\ldots+h^{n}-\cancel{x^{n}}}{h}\\
& =\lim_{h\to0}\frac{\binom{n}{1}x^{n-1}h^{1}+\binom{n}{2}x^{n-2}h^{2}+\binom{n}{3}x^{3}h^{3}+\ldots+h^{n}}{h}\\
& =\lim_{h\to0}\binom{n}{1}x^{n-1}+\binom{n}{2}x^{n-2}h^{1}+\binom{n}{3}x^{3}h^{2}+\ldots+h^{n-1}\\
& =\binom{n}{1}x^{n-1}\\
& =\frac{n!}{(n-1)!1!}x^{n-1}\\
& =\frac{n(n-1)!}{(n-1)!}x^{n-1}\\
& =nx^{n-1}
\end{align*}
d x d ( x n ) = h → 0 lim h ( x + h ) n − x n = h → 0 lim h x n + ( 1 n ) x n − 1 h 1 + ( 2 n ) x n − 2 h 2 + ( 3 n ) x 3 h 3 + … + h n − x n = h → 0 lim h ( 1 n ) x n − 1 h 1 + ( 2 n ) x n − 2 h 2 + ( 3 n ) x 3 h 3 + … + h n = h → 0 lim ( 1 n ) x n − 1 + ( 2 n ) x n − 2 h 1 + ( 3 n ) x 3 h 2 + … + h n − 1 = ( 1 n ) x n − 1 = ( n − 1 )! 1 ! n ! x n − 1 = ( n − 1 )! n ( n − 1 )! x n − 1 = n x n − 1
Derivasi dari x n x^n x n d ( x n ) x = n x n − 1 \dfrac{d(x^n)}{x} = nx^{n-1} x d ( x n ) = n x n − 1
Sifat Perkalian dengan Konstanta
Misalkan kita menggambar fungsi y 1 = f ( x ) y_1=f(x) y 1 = f ( x ) y 2 = 3 f ( x ) y_2=3f(x) y 2 = 3 f ( x ) y y y x x x 3 f ( x ) d x = 3 d f d x \dfrac{3f(x)}{dx} = 3\dfrac{df}{dx} d x 3 f ( x ) = 3 d x df c f ( x ) d x = c d f d x \dfrac{cf(x)}{dx} = c\dfrac{df}{dx} d x c f ( x ) = c d x df c c c
Bukti dengan limit:
g ( x ) = c f ( x ) d g d x = lim h → 0 g ( x + h ) − g ( x ) h = lim h → 0 c f ( x + h ) − c f ( x ) h = lim h → 0 c ( f ( x + h ) − f ( x ) h ) d g d x = c lim h → 0 f ( x + h ) − f ( x ) h d ( c f ( x ) ) d x = c d f d x \begin{align*}
g(x) & =cf(x)\\
\frac{dg}{dx} & =\lim_{h\to0}\frac{g(x+h)-g(x)}{h}\\
& =\lim_{h\to0}\frac{cf(x+h)-cf(x)}{h}\\
& =\lim_{h\to0}c\left(\frac{f(x+h)-f(x)}{h}\right)\\
\frac{dg}{dx} & =c\lim_{h\to0}\frac{f(x+h)-f(x)}{h}\\
\frac{d(cf(x))}{dx} & =c\frac{df}{dx}
\end{align*}
g ( x ) d x d g d x d g d x d ( c f ( x )) = c f ( x ) = h → 0 lim h g ( x + h ) − g ( x ) = h → 0 lim h c f ( x + h ) − c f ( x ) = h → 0 lim c ( h f ( x + h ) − f ( x ) ) = c h → 0 lim h f ( x + h ) − f ( x ) = c d x df
c c c c c c h h h
Sifat perkalian dengan konstanta pada derivasid ( c f ( x ) ) d x = c d f d x \dfrac{d(cf(x))}{dx}=c\dfrac{df}{dx} d x d ( c f ( x )) = c d x df c c c
Sifat Penjumlahan
Misalkan kita menggambar grafik fungsi y 1 = f ( x ) y_1 = f(x) y 1 = f ( x ) y 2 = g ( x ) y_2=g(x) y 2 = g ( x ) y 3 = f ( x ) + g ( x ) y_3 = f(x) + g(x) y 3 = f ( x ) + g ( x ) y y y y y y x x x
Saat perubahan x x x x x x y y y y y y
Saat kita membuat garis singgung pada ketiga grafik fungsi pada posisi sama, seharusnya gradien
garis singgung fungsi ketiga sama dengan penjumlahan gradien garis singgung fungsi pertama dan
kedua.
Maka d ( f ( x ) + g ( x ) ) d x = d f d x + d g d x \dfrac{d(f(x) + g(x))}{dx}=\dfrac{df}{dx} + \dfrac{dg}{dx} d x d ( f ( x ) + g ( x )) = d x df + d x d g
Bukti dengan limit:
d ( f ( x ) + g ( x ) ) d x = lim h → 0 f ( x + h ) + g ( x + h ) − f ( x ) − g ( x ) h = lim h → 0 f ( x + h ) − f ( x ) h + g ( x + h ) − g ( x ) h = lim h → 0 ( f ( x + h ) − f ( x ) h ) + lim h → 0 ( g ( x + h ) − g ( x ) h ) = d f d x + d g d x \begin{align*}
\frac{d(f(x)+g(x))}{dx} & =\lim_{h\to0}\frac{f(x+h)+g(x+h)-f(x)-g(x)}{h}\\
& =\lim_{h\to0}\frac{f(x+h)-f(x)}{h}+\frac{g(x+h)-g(x)}{h}\\
& =\lim_{h\to0}\left(\frac{f(x+h)-f(x)}{h}\right)+\lim_{h\to0}\left(\frac{g(x+h)-g(x)}{h}\right)\\
& =\frac{df}{dx}+\frac{dg}{dx}
\end{align*}
d x d ( f ( x ) + g ( x )) = h → 0 lim h f ( x + h ) + g ( x + h ) − f ( x ) − g ( x ) = h → 0 lim h f ( x + h ) − f ( x ) + h g ( x + h ) − g ( x ) = h → 0 lim ( h f ( x + h ) − f ( x ) ) + h → 0 lim ( h g ( x + h ) − g ( x ) ) = d x df + d x d g
Sifat Perkalian
Misal kita membuat segi panjang dengan panjang f ( x ) f(x) f ( x ) g ( x ) g(x) g ( x ) x x x f ( x ) . g ( x ) f(x).g(x) f ( x ) . g ( x )
Saat kita meningkatkan nilai x x x d f df df d g dg d g
Δ L = f ( x ) d g + g ( x ) d f + d g × d f \Delta L = f(x)dg + g(x)df + dg\times df
Δ L = f ( x ) d g + g ( x ) df + d g × df
Pertambahan luas adalah pertambahan nilai f ( x ) g ( x ) f(x)g(x) f ( x ) g ( x )
d ( f ( x ) g ( x ) ) = f ( x ) d g + g ( x ) d f + d g d f d(f(x)g(x)) = f(x)dg + g(x)df + dgdf
d ( f ( x ) g ( x )) = f ( x ) d g + g ( x ) df + d g df
Saat perubahan nilai x x x d f df df d g dg d g d f × d g df\times dg df × d g
d ( f ( x ) g ( x ) ) = f ( x ) d g + g ( x ) d f d(f(x)g(x)) = f(x)dg + g(x)df
d ( f ( x ) g ( x )) = f ( x ) d g + g ( x ) df
Bukti dengan limit:
d ( f ( x ) g ( x ) ) d x = lim h → 0 f ( x + h ) g ( x + h ) − f ( x ) g ( x ) h = lim h → 0 f ( x + h ) g ( x + h ) − f ( x ) g ( x + h ) + f ( x ) g ( x + h ) − f ( x ) g ( x ) h = lim h → 0 ( f ( x + h ) − f ( x ) ) g ( x + h ) + f ( x ) ( g ( x + h ) − g ( x ) ) h = lim h → 0 ( ( f ( x + h ) − f ( x ) ) g ( x + h ) h ) + lim h → 0 ( f ( x ) ( g ( x + h ) − g ( x ) ) h ) = lim h → 0 ( f ( x + h ) − f ( x ) h ) lim h → 0 ( g ( x + h ) ) + lim h → 0 ( f ( x ) ) lim h → 0 ( g ( x + h ) − g ( x ) h ) = d f d x g ( x ) + f ( x ) d g d x \begin{align*}
\frac{d(f(x)g(x))}{dx} & =\lim_{h\to0}\frac{f(x+h)g(x+h)-f(x)g(x)}{h}\\
& =\lim_{h\to0}\frac{f(x+h)g(x+h)\boxed{-f(x)g(x+h)+f(x)g(x+h)}-f(x)g(x)}{h}\\
& =\lim_{h\to0}\frac{(f(x+h)\boxed{-f(x)})g(x+h)+f(x)(\boxed{g(x+h)}-g(x))}{h}\\
& =\lim_{h\to0}\left(\frac{(f(x+h)-f(x))g(x+h)}{h}\right)+\lim_{h\to0}\left(\frac{f(x)(g(x+h)-g(x))}{h}\right)\\
& =\lim_{h\to0}\left(\frac{f(x+h)-f(x)}{h}\right)\lim_{h\to0}\left(g(x+h)\right)+\lim_{h\to0}\left(f(x)\right)\lim_{h\to0}\left(\frac{g(x+h)-g(x)}{h}\right)\\
& =\frac{df}{dx}g(x)+f(x)\frac{dg}{dx}
\end{align*}
d x d ( f ( x ) g ( x )) = h → 0 lim h f ( x + h ) g ( x + h ) − f ( x ) g ( x ) = h → 0 lim h f ( x + h ) g ( x + h ) − f ( x ) g ( x + h ) + f ( x ) g ( x + h ) − f ( x ) g ( x ) = h → 0 lim h ( f ( x + h ) − f ( x ) ) g ( x + h ) + f ( x ) ( g ( x + h ) − g ( x )) = h → 0 lim ( h ( f ( x + h ) − f ( x )) g ( x + h ) ) + h → 0 lim ( h f ( x ) ( g ( x + h ) − g ( x )) ) = h → 0 lim ( h f ( x + h ) − f ( x ) ) h → 0 lim ( g ( x + h ) ) + h → 0 lim ( f ( x ) ) h → 0 lim ( h g ( x + h ) − g ( x ) ) = d x df g ( x ) + f ( x ) d x d g
Aturan perkalian pada derivasi:d ( f ( x ) g ( x ) ) d x = d f d x g ( x ) + f ( x ) d g d x \dfrac{d(f(x)g(x))}{dx} =\dfrac{df}{dx}g(x)+f(x)\dfrac{dg}{dx} d x d ( f ( x ) g ( x )) = d x df g ( x ) + f ( x ) d x d g Kiri × dKanan + Kanan × dKiri \text{Kiri}\times\text{dKanan} + \text{Kanan}\times\text{dKiri} Kiri × dKanan + Kanan × dKiri
Aturan Rantai (Chain Rule)
Aturan ini digunakan untuk mencari derivasi dari sebuah komposisi fungsi. Misalkan kita ingin
mencari derivasi dari d ( sin ( 2 x ) ) d x \dfrac{d(\sin(2x))}{dx} d x d ( sin ( 2 x )) x x x 2 x 2x 2 x sin ( 2 x ) \sin(2x) sin ( 2 x ) 2 x = h 2x=h 2 x = h sin ( 2 x ) = sin ( h ) \sin(2x)=\sin(h) sin ( 2 x ) = sin ( h ) sin ( h ) \sin(h) sin ( h ) h h h
d ( sin ( h ) ) d h = cos ( h ) \frac{d(\sin(h))}{dh}=\cos(h)
d h d ( sin ( h )) = cos ( h )
Persamaan bisa disusun ulang sebagai:
d ( sin ( h ) ) = cos ( h ) d h (1) d(\sin(h))=\cos(h)dh \tag{1}
d ( sin ( h )) = cos ( h ) d h ( 1 )
Kemudian kita bisa mencari derivasi dari h h h x x x
d h d x = d ( 2 x ) d x d h d x = 2 \begin{align*}
\frac{dh}{dx} &= \frac{d(2x)}{dx} \\
\frac{dh}{dx} &= 2
\end{align*}
d x d h d x d h = d x d ( 2 x ) = 2
Persamaan bisa disusun ulang sebagai:
d h = 2 d x (2) dh = 2dx \tag{2}
d h = 2 d x ( 2 )
Masukan persamaan 2 ke persamaan 1.
d ( sin ( h ) ) = cos ( h ) d h = cos ( h ) 2 d x = 2 cos ( h ) d x \begin{align*}
d(\sin(h))&=\cos(h)dh\\
&= \cos(h)2dx\\
&= 2\cos(h)dx
\end{align*}
d ( sin ( h )) = cos ( h ) d h = cos ( h ) 2 d x = 2 cos ( h ) d x
Persamaan bisa disusun ulang ke bentuk d ( sin ( 2 x ) ) d x \dfrac{d(\sin(2x))}{dx} d x d ( sin ( 2 x )) h h h
d ( sin ( h ) ) d x = 2 cos ( h ) d ( sin ( 2 h ) ) d x = 2 cos ( 2 x ) \begin{align*}
\frac{d(\sin(h))}{dx} = 2\cos(h)\\
\frac{d(\sin(2h))}{dx} = 2\cos(2x)\\
\end{align*}
d x d ( sin ( h )) = 2 cos ( h ) d x d ( sin ( 2 h )) = 2 cos ( 2 x )
Lebih umum
Misalkan kita mencari derivasi dari d ( f ( g ( x ) ) ) d x \dfrac{d(f(g(x)))}{dx} d x d ( f ( g ( x )))
Misalkan h = g ( x ) h=g(x) h = g ( x ) f ( h ) f(h) f ( h ) h h h
d ( f ( h ) ) d h = d f d h \frac{d(f(h))}{dh} = \frac{df}{dh}
d h d ( f ( h )) = d h df
Persamaan disusun ulang:
d ( f ( h ) ) = d f d h d h (1) d(f(h)) = \frac{df}{dh} dh \tag{1}
d ( f ( h )) = d h df d h ( 1 )
Derivasi h h h x x x
d h d x = d g d x d h = d g d x d x \begin{align*}
\frac{dh}{dx}&=\frac{dg}{dx}\\
dh &= \frac{dg}{dx} dx \tag{2}
\end{align*}
d x d h d h = d x d g = d x d g d x ( 2 )
Masukkan persamaan 2 ke 1
d ( f ( h ) ) = d f d h d h = d f d h d g d x d x \begin{align*}
d(f(h)) &= \frac{df}{dh} dh\\
&= \frac{df}{dh} \frac{dg}{dx} dx
\end{align*}
d ( f ( h )) = d h df d h = d h df d x d g d x
Persamaan disusun ulang dan nilai h h h
d ( f ( h ) ) d x = d f d h d g d x d ( f ( g ( x ) ) ) d x = d f d g d g d x \begin{align*}
\frac{d(f(h))}{dx} &= \frac{df}{dh} \frac{dg}{dx}\\
\frac{d(f(g(x)))}{dx} &= \frac{df}{dg} \frac{dg}{dx}\\
\end{align*}
d x d ( f ( h )) d x d ( f ( g ( x ))) = d h df d x d g = d g df d x d g
Aturan rantai pada derivatifd ( f ( g ( x ) ) ) d x = d f d g d g d x \dfrac{d(f(g(x)))}{dx} = \dfrac{df}{dg} \dfrac{dg}{dx} d x d ( f ( g ( x ))) = d g df d x d g d f d g \dfrac{df}{dg} d g df f ( g ( x ) ) f(g(x)) f ( g ( x )) g ( x ) g(x) g ( x ) g ( x ) g(x) g ( x ) d g d x \dfrac{dg}{dx} d x d g g ( x ) g(x) g ( x ) x x x x x x
d ( Luar ( Dalam ( x ) ) ) d x = d Luar d Dalam . d Dalam d x \displaystyle{ \frac{ d \left( \text{Luar} \left( \text{Dalam} \left( x \right) \right) \right) }{ {\text{d}x} } = \frac{ d \text{Luar} }{ d \text{Dalam} } . \frac{ d \text{Dalam} }{ {\text{d}x} } } d x d ( Luar ( Dalam ( x ) ) ) = d Dalam d Luar . d x d Dalam
Aturan Pembagian
Kita menggunakan sifat perkalian, aturan rantai dan sifat eksponen untuk menurunkan aturan ini.
d d x ( f ( x ) g ( x ) ) = d d x ( f ( x ) 1 g ( x ) ) = d d x ( f ( x ) g ( x ) − 1 ) = f ( x ) d ( g ( x ) − 1 ) d x + g ( x ) − 1 d ( f ( x ) ) d x \begin{align*}
\frac{d}{dx}\left(\frac{f\left(x\right)}{g\left(x\right)}\right) & =\frac{d}{dx}\left(f\left(x\right)\frac{1}{g\left(x\right)}\right)\\
& =\frac{d}{dx}\left(f\left(x\right)g\left(x\right)^{-1}\right)\\
& =f(x)\frac{d\left(g\left(x\right)^{-1}\right)}{dx}+g\left(x\right)^{-1}\frac{d\left(f(x)\right)}{dx}
\end{align*}
d x d ( g ( x ) f ( x ) ) = d x d ( f ( x ) g ( x ) 1 ) = d x d ( f ( x ) g ( x ) − 1 ) = f ( x ) d x d ( g ( x ) − 1 ) + g ( x ) − 1 d x d ( f ( x ) )
Sekarang kita harus mencari d ( g ( x ) − 1 ) d x \dfrac{d\left(g\left(x\right)^{-1}\right)}{dx} d x d ( g ( x ) − 1 ) g ( x ) − 1 g(x)^{-1} g ( x ) − 1
h ( g ( x ) ) = g ( x ) − 1 h ( x ) = x − 1 \begin{align*}
h\left(g\left(x\right)\right) & =g\left(x\right)^{-1}\\
h(x) & =x^{-1}
\end{align*}
h ( g ( x ) ) h ( x ) = g ( x ) − 1 = x − 1
Maka
d ( g ( x ) − 1 ) d x = d ( h ( g ( x ) ) ) d x \frac{d\left(g\left(x\right)^{-1}\right)}{dx} =\frac{d\left(h\left(g\left(x\right)\right)\right)}{dx}
d x d ( g ( x ) − 1 ) = d x d ( h ( g ( x ) ) )
Sekarang kita bisa menggunakan aturan rantai:
d ( g ( x ) − 1 ) d x = d h d g d g d x d h d x = − 1 x − 2 d h d g = − 1 g ( x ) − 2 d ( g ( x ) − 1 ) d x = d h d g d g d x = − g ( x ) − 2 d g d x \begin{align*}
\frac{d\left(g\left(x\right)^{-1}\right)}{dx} & =\frac{dh}{dg}\frac{dg}{dx}\\
\frac{dh}{dx} & =-1x^{-2}\\
\frac{dh}{dg} & =-1g\left(x\right)^{-2}\\
\frac{d\left(g\left(x\right)^{-1}\right)}{dx} & =\frac{dh}{dg}\frac{dg}{dx}\\
& =-g(x)^{-2}\frac{dg}{dx}
\end{align*}
d x d ( g ( x ) − 1 ) d x d h d g d h d x d ( g ( x ) − 1 ) = d g d h d x d g = − 1 x − 2 = − 1 g ( x ) − 2 = d g d h d x d g = − g ( x ) − 2 d x d g
Sekarang kita bisa memasukkan persamaan ini ke persamaan derivatif pembagian.
d d x ( f ( x ) g ( x ) ) = f ( x ) d ( g ( x ) − 1 ) d x + g ( x ) − 1 d ( f ( x ) ) d x = − f ( x ) g ( x ) − 2 d g d x + g ( x ) − 1 d f d x = − f ( x ) d g d x g ( x ) 2 + ( d f d x ) g ( x ) = ( d f d x ) g ( x ) − f ( x ) d g d x g ( x ) 2 = ( d f d x ) g ( x ) × g ( x ) g ( x ) − f ( x ) d g d x g ( x ) 2 = d f d x g ( x ) g ( x ) 2 − f ( x ) d g d x g ( x ) 2 = d f d x g ( x ) − f ( x ) d g d x g ( x ) 2 = d f d x g ( x ) − d g d x f ( x ) g ( x ) 2 \begin{align*}
\frac{d}{dx}\left(\frac{f\left(x\right)}{g\left(x\right)}\right) & =f(x)\frac{d\left(g\left(x\right)^{-1}\right)}{dx}+g\left(x\right)^{-1}\frac{d\left(f(x)\right)}{dx}\\
& =-f(x)g(x)^{-2}\frac{dg}{dx}+g\left(x\right)^{-1}\frac{df}{dx}\\
& =\frac{-f(x)\dfrac{dg}{dx}}{g(x)^{2}}+\frac{\left(\dfrac{df}{dx}\right)}{g\left(x\right)}\\
& =\frac{\left(\dfrac{df}{dx}\right)}{g\left(x\right)}-\frac{f(x)\dfrac{dg}{dx}}{g(x)^{2}}\\
& =\frac{\left(\dfrac{df}{dx}\right)}{g\left(x\right)}\times\frac{g(x)}{g(x)}-\frac{f(x)\dfrac{dg}{dx}}{g(x)^{2}}\\
& =\frac{\dfrac{df}{dx}g\left(x\right)}{g\left(x\right)^{2}}-\frac{f(x)\dfrac{dg}{dx}}{g(x)^{2}}\\
& =\frac{\dfrac{df}{dx}g\left(x\right)-f(x)\dfrac{dg}{dx}}{g\left(x\right)^{2}}\\
& =\frac{\dfrac{df}{dx}g\left(x\right)-\dfrac{dg}{dx}f(x)}{g\left(x\right)^{2}}
\end{align*}
d x d ( g ( x ) f ( x ) ) = f ( x ) d x d ( g ( x ) − 1 ) + g ( x ) − 1 d x d ( f ( x ) ) = − f ( x ) g ( x ) − 2 d x d g + g ( x ) − 1 d x df = g ( x ) 2 − f ( x ) d x d g + g ( x ) ( d x df ) = g ( x ) ( d x df ) − g ( x ) 2 f ( x ) d x d g = g ( x ) ( d x df ) × g ( x ) g ( x ) − g ( x ) 2 f ( x ) d x d g = g ( x ) 2 d x df g ( x ) − g ( x ) 2 f ( x ) d x d g = g ( x ) 2 d x df g ( x ) − f ( x ) d x d g = g ( x ) 2 d x df g ( x ) − d x d g f ( x )
Sifat pembagian pada derivasid d x ( f ( x ) g ( x ) ) = d f d x g ( x ) − d g d x f ( x ) g ( x ) 2 \dfrac{d}{dx}\left(\dfrac{f\left(x\right)}{g\left(x\right)}\right) =\dfrac{\dfrac{df}{dx}g\left(x\right)-\dfrac{dg}{dx}f(x)}{g\left(x\right)^{2}} d x d ( g ( x ) f ( x ) ) = g ( x ) 2 d x df g ( x ) − d x d g f ( x ) dAtas × Bawah − dBawah × Atas Bawah 2 \dfrac{\text{dAtas}\times\text{Bawah}-\text{dBawah}\times\text{Atas}}{\text{Bawah}^2} Bawah 2 dAtas × Bawah − dBawah × Atas
Sifat Perpangkatkan/Eksponen
Misalnya kita ingin mencari derivasi dari f ( x ) = 2 x f(x) = 2^x f ( x ) = 2 x
d f d x = lim h → 0 2 x + h − 2 x h = lim h → 0 2 x 2 h − 2 x h = lim h → 0 2 x ( 2 h − 1 ) h = 2 x ( lim h → 0 2 h − 1 h ) \begin{align*}
\frac{df}{dx} & =\lim_{h\to0}\frac{2^{x+h}-2^{x}}{h}\\
& =\lim_{h\to0}\frac{2^{x}2^{h}-2^{x}}{h}\\
& =\lim_{h\to0}2^{x}\frac{(2^{h}-1)}{h}\\
& =2^{x}\left(\lim_{h\to0}\frac{2^{h}-1}{h}\right)
\end{align*}
d x df = h → 0 lim h 2 x + h − 2 x = h → 0 lim h 2 x 2 h − 2 x = h → 0 lim 2 x h ( 2 h − 1 ) = 2 x ( h → 0 lim h 2 h − 1 )
Jika dihitung dengan kalkulator nilai dari
lim h → 0 2 h − 1 h ≈ 0.69 \lim_{h\to0}\frac{2^{h}-1}{h} \approx 0.69
h → 0 lim h 2 h − 1 ≈ 0.69
Maka bisa dikatakan derivasi dari fungsi eksponen merupakan fungsi tersebut dikali dengan konstanta
aneh. Kita perlu basis yang jika dicari derivasinya akan menghasilkan konstanta bernilai 1.
Kita coba jika basisnya adalah 3.
lim h → 0 3 h − 1 h ≈ 1.01 \lim_{h\to0}\frac{3^{h}-1}{h} \approx 1.01
h → 0 lim h 3 h − 1 ≈ 1.01
Saat kita menggunakan basis 2 konstantanya 0.69. Saat kita menggunakan basis 3 konstantanya 1.01.
Basis yang menghasilkan konstanta 1 seharusnya di bawah 3, di atas 2 dan lebih dekat dengan 3
daripada 2. Basis itu adalah e ≈ 2.7 e\approx2.7 e ≈ 2.7
d ( e x ) d x = e x ( lim h → 0 e h − 1 h ) \frac{d(e^x)}{dx} = e^{x}\left(\lim_{h\to0}\frac{e^{h}-1}{h}\right)
d x d ( e x ) = e x ( h → 0 lim h e h − 1 )
Kita harus mengingat definisi e e e
e = lim n → ∞ ( 1 + 1 n ) n e =\lim_{n\to\infty}\left(1+\frac{1}{n}\right)^{n}
e = n → ∞ lim ( 1 + n 1 ) n
Misal h = 1 n h=\dfrac{1}{n} h = n 1 n → ∞ n \to \infty n → ∞ 1 n \dfrac{1}{n} n 1 h → 0 h \to 0 h → 0
e = lim h → 0 ( 1 + h ) 1 h e =\lim_{h\to0}\left(1+h\right)^{\frac{1}{h}}
e = h → 0 lim ( 1 + h ) h 1
Kita bisa memasukkan ini ke persamaan tadi.
d ( e x ) d x = e x ( lim h → 0 ( lim h → 0 ( 1 + h ) 1 h ) h − 1 h ) = e x ( lim h → 0 ( ( 1 + h ) 1 h ) h − 1 h ) = e x ( lim h → 0 ( 1 + h ) 1 h × h − 1 h ) = e x ( lim h → 0 ( 1 + h ) 1 − 1 h ) = e x ( lim h → 0 1 + h − 1 h ) = e x ( lim h → 0 h h ) = e x ( lim h → 0 1 ) = e x \begin{align*}
\frac{d(e^{x})}{dx} & =e^{x}\left(\lim_{h\to0}\frac{\left(\lim_{h\to0}\left(1+h\right)^{\frac{1}{h}}\right)^{h}-1}{h}\right)\\
& =e^{x}\left(\lim_{h\to0}\frac{\left(\left(1+h\right)^{\frac{1}{h}}\right)^{h}-1}{h}\right)\\
& =e^{x}\left(\lim_{h\to0}\frac{\left(1+h\right)^{\frac{1}{h}\times h}-1}{h}\right)\\
& =e^{x}\left(\lim_{h\to0}\frac{\left(1+h\right)^{1}-1}{h}\right)\\
& =e^{x}\left(\lim_{h\to0}\frac{1+h-1}{h}\right)\\
& =e^{x}\left(\lim_{h\to0}\frac{h}{h}\right)\\
& =e^{x}\left(\lim_{h\to0}1\right)\\
& =e^{x}
\end{align*}
d x d ( e x ) = e x h → 0 lim h ( lim h → 0 ( 1 + h ) h 1 ) h − 1 = e x h → 0 lim h ( ( 1 + h ) h 1 ) h − 1 = e x ( h → 0 lim h ( 1 + h ) h 1 × h − 1 ) = e x ( h → 0 lim h ( 1 + h ) 1 − 1 ) = e x ( h → 0 lim h 1 + h − 1 ) = e x ( h → 0 lim h h ) = e x ( h → 0 lim 1 ) = e x
Maka kita bisa mencari derivasi dari 2 x 2^x 2 x e ln ( x ) = x e^{\ln(x)}=x e l n ( x ) = x e ln ( 2 ) = 2 e^{\ln(2)}=2 e l n ( 2 ) = 2
d ( 2 x ) d x = d ( ( e ln ( 2 ) ) x ) d x = d ( e x ln ( 2 ) ) d x \begin{align*}
\frac{d(2^{x})}{dx} &=\frac{d\left(\left(e^{\ln(2)}\right)^{x}\right)}{dx}\\
&=\frac{d\left(e^{x\ln(2)}\right)}{dx}
\end{align*}
d x d ( 2 x ) = d x d ( ( e l n ( 2 ) ) x ) = d x d ( e x l n ( 2 ) )
e x ln ( 2 ) e^{x\ln(2)} e x l n ( 2 )
g ( x ) = x ln ( 2 ) f ( g ( x ) = e x ln ( 2 ) f ( x ) = e x \begin{align*}
g(x) & =x\ln(2)\\
f(g(x) & =e^{x\ln(2)}\\
f(x) & =e^{x}
\end{align*}
g ( x ) f ( g ( x ) f ( x ) = x ln ( 2 ) = e x l n ( 2 ) = e x
Kita bisa menari derivasinya lagi menggunakan aturan rantai.
d ( 2 x ) d x = d ( e x ln ( 2 ) ) d x = d ( f ( g ( x ) ) ) d x = d f d g d g d x d f d x = e x d f d g = e g ( x ) = e x ln ( 2 ) d g d x = ln ( 2 ) d ( 2 x ) d x = d f d g d g d x = e x ln ( 2 ) ln ( 2 ) = ( e ln ( 2 ) ) x ln ( 2 ) = 2 x ln ( 2 ) \begin{align*}
\frac{d(2^{x})}{dx} & =\frac{d\left(e^{x\ln(2)}\right)}{dx}\\
& =\frac{d(f(g(x)))}{dx}\\
& =\frac{df}{dg}\frac{dg}{dx}\\
\frac{df}{dx} & =e^{x}\\
\frac{df}{dg} & =e^{g(x)}\\
& =e^{x\ln(2)}\\
\frac{dg}{dx} & =\ln(2)\\
\frac{d(2^{x})}{dx} & =\frac{df}{dg}\frac{dg}{dx}\\
& =e^{x\ln(2)}\ln(2)\\
& =\left(e^{\ln(2)}\right)^{x}\ln(2)\\
& =2^{x}\ln(2)
\end{align*}
d x d ( 2 x ) d x df d g df d x d g d x d ( 2 x ) = d x d ( e x l n ( 2 ) ) = d x d ( f ( g ( x ))) = d g df d x d g = e x = e g ( x ) = e x l n ( 2 ) = ln ( 2 ) = d g df d x d g = e x l n ( 2 ) ln ( 2 ) = ( e l n ( 2 ) ) x ln ( 2 ) = 2 x ln ( 2 )
Kenyataanya ln ( 2 ) ≈ 0.69 \ln(2)\approx0.69 ln ( 2 ) ≈ 0.69
Lebih umum:
d ( a x ) d x = d ( ( e ln ( a ) ) x ) d x = d ( e x ln ( a ) ) d x \begin{align*}
\frac{d(a^{x})}{dx} &=\frac{d\left(\left(e^{\ln(a)}\right)^{x}\right)}{dx}\\
&=\frac{d\left(e^{x\ln(a)}\right)}{dx}
\end{align*}
d x d ( a x ) = d x d ( ( e l n ( a ) ) x ) = d x d ( e x l n ( a ) )
e x ln ( a ) e^{x\ln(a)} e x l n ( a )
g ( x ) = x ln ( a ) f ( g ( x ) = e x ln ( a ) f ( x ) = e x \begin{align*}
g(x) & =x\ln(a)\\
f(g(x) & =e^{x\ln(a)}\\
f(x) & =e^{x}
\end{align*}
g ( x ) f ( g ( x ) f ( x ) = x ln ( a ) = e x l n ( a ) = e x
Kita bisa mencari derivasi a x a^x a x
d ( a x ) d x = d ( e x ln ( a ) ) d x = d ( f ( g ( x ) ) ) d x = d f d g d g d x d f d x = e x d f d g = e g ( x ) = e x ln ( a ) d g d x = ln ( a ) d ( a x ) d x = d f d g d g d x = e x ln ( a ) ln ( a ) = ( e ln ( a ) ) x ln ( a ) = a x ln ( a ) \begin{align*}
\frac{d(a^{x})}{dx} & =\frac{d\left(e^{x\ln(a)}\right)}{dx}\\
& =\frac{d(f(g(x)))}{dx}\\
& =\frac{df}{dg}\frac{dg}{dx}\\
\frac{df}{dx} & =e^{x}\\
\frac{df}{dg} & =e^{g(x)}\\
& =e^{x\ln(a)}\\
\frac{dg}{dx} & =\ln(a)\\
\frac{d(a^{x})}{dx} & =\frac{df}{dg}\frac{dg}{dx}\\
& =e^{x\ln(a)}\ln(a)\\
& =\left(e^{\ln(a)}\right)^{x}\ln(a)\\
& =a^{x}\ln(a)
\end{align*}
d x d ( a x ) d x df d g df d x d g d x d ( a x ) = d x d ( e x l n ( a ) ) = d x d ( f ( g ( x ))) = d g df d x d g = e x = e g ( x ) = e x l n ( a ) = ln ( a ) = d g df d x d g = e x l n ( a ) ln ( a ) = ( e l n ( a ) ) x ln ( a ) = a x ln ( a )
Sifat eksponen pada derivasi. Misalkan a a a a x d x = ln ( a ) a x \dfrac{a^x}{dx} = \ln(a)a^x d x a x = ln ( a ) a x e x d x = e x \dfrac{e^x}{dx} = e^x d x e x = e x
Derivasi dari Logaritma
Misalkan kita ingin mencari derivasi dari log a ( x ) \log_a(x) log a ( x )
d ( log a ( x ) ) d x = lim h → 0 log a ( x + h ) − log a ( x ) h = lim h → 0 1 h log a ( x + h x ) = lim h → 0 1 h log a ( 1 + h x ) = lim h → 0 log a ( ( 1 + h x ) 1 h ) = log a ( lim h → 0 ( 1 + h x ) 1 h ) \begin{align*}
\frac{d(\log_{a}(x))}{dx} & =\lim_{h\to0}\frac{\log_{a}(x+h)-\log_{a}(x)}{h}\\
& =\lim_{h\to0}\frac{1}{h}\log_{a}\left(\frac{x+h}{x}\right)\\
& =\lim_{h\to0}\frac{1}{h}\log_{a}\left(1+\frac{h}{x}\right)\\
& =\lim_{h\to0}\log_{a}\left(\left(1+\frac{h}{x}\right)^{\frac{1}{h}}\right)\\
& =\log_{a}\left(\lim_{h\to0}\left(1+\frac{h}{x}\right)^{\frac{1}{h}}\right)
\end{align*}
d x d ( log a ( x )) = h → 0 lim h log a ( x + h ) − log a ( x ) = h → 0 lim h 1 log a ( x x + h ) = h → 0 lim h 1 log a ( 1 + x h ) = h → 0 lim log a ( ( 1 + x h ) h 1 ) = log a ( h → 0 lim ( 1 + x h ) h 1 )
Bentuk di dalam limit mirip dengan definisi e e e
e = lim n → ∞ ( 1 + 1 n ) n e =\lim_{n\to\infty}\left(1+\frac{1}{n}\right)^{n}
e = n → ∞ lim ( 1 + n 1 ) n
Anggap h x = m \dfrac{h}{x}=m x h = m h = m x h=mx h = m x h → 0 h\to 0 h → 0 h x → 0 \dfrac{h}{x} \to 0 x h → 0 m → 0 m \to 0 m → 0
d ( log a ( x ) ) d x = log a ( lim m → 0 ( 1 + m ) 1 m x ) = log a ( lim m → 0 ( ( 1 + m ) 1 m ) 1 x ) = log a ( ( lim m → 0 ( 1 + m ) 1 m ) 1 x ) \begin{align*}
\frac{d(\log_{a}(x))}{dx} & =\log_{a}\left(\lim_{m\to0}\left(1+m\right)^{\frac{1}{mx}}\right)\\
& =\log_{a}\left(\lim_{m\to0}\left(\left(1+m\right)^{\frac{1}{m}}\right)^{\frac{1}{x}}\right)\\
& =\log_{a}\left(\left(\lim_{m\to0}\left(1+m\right)^{\frac{1}{m}}\right)^{\frac{1}{x}}\right)
\end{align*}
d x d ( log a ( x )) = log a ( m → 0 lim ( 1 + m ) m x 1 ) = log a ( m → 0 lim ( ( 1 + m ) m 1 ) x 1 ) = log a ( ( m → 0 lim ( 1 + m ) m 1 ) x 1 )
lim m → 0 ( 1 + m ) 1 m \lim_{m\to0}\left(1+m\right)^{\frac{1}{m}} lim m → 0 ( 1 + m ) m 1 e e e n n n m m m
d ( log a ( x ) ) d x = log a ( e 1 x ) = 1 x log a ( e ) \begin{align*}
\frac{d(\log_{a}(x))}{dx} & =\log_{a}\left(e^{\frac{1}{x}}\right)\\
& =\frac{1}{x}\log_{a}\left(e\right)
\end{align*}
d x d ( log a ( x )) = log a ( e x 1 ) = x 1 log a ( e )
Bentuk log a ( e ) \log_{a}\left(e\right) log a ( e ) log k ( e ) log k ( a ) \dfrac{\log_{k}(e)}{\log_{k}(a)} log k ( a ) log k ( e ) k k k k = e k = e k = e
d ( log a ( x ) ) d x = 1 x log a ( e ) = 1 x log e ( e ) log e ( a ) = 1 x 1 ln ( a ) = 1 x ln ( a ) \begin{align*}
\frac{d(\log_{a}(x))}{dx} & =\frac{1}{x}\log_{a}\left(e\right)\\
& =\frac{1}{x}\frac{\log_{e}(e)}{\log_{e}(a)}\\
& =\frac{1}{x}\frac{1}{\ln(a)}\\
& =\frac{1}{x\ln(a)}
\end{align*}
d x d ( log a ( x )) = x 1 log a ( e ) = x 1 log e ( a ) log e ( e ) = x 1 ln ( a ) 1 = x ln ( a ) 1
Sekarang kita bisa mencari turunan dari logaritma natural.
d ( ln ( x ) ) d x = d ( log e ( x ) ) d x = 1 x ln ( e ) = 1 x \begin{align*}
\frac{d(\ln(x))}{dx} & =\frac{d(\log_{e}(x))}{dx}\\
& =\frac{1}{x\ln(e)}\\
& =\frac{1}{x}
\end{align*}
d x d ( ln ( x )) = d x d ( log e ( x )) = x ln ( e ) 1 = x 1
Derivasi dari logaritmad ( log a ( x ) ) d x = 1 x ln ( a ) \dfrac{d(\log_{a}(x))}{dx} =\dfrac{1}{x\ln(a)} d x d ( log a ( x )) = x ln ( a ) 1 d ( ln ( x ) ) d x = 1 x \dfrac{d(\ln(x))}{dx} =\dfrac{1}{x} d x d ( ln ( x )) = x 1