Persamaan Sinus
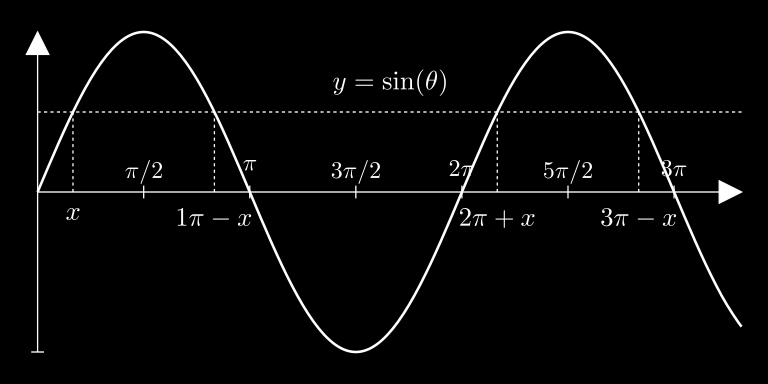
Fungsi sinus akan berulang setelah 360 d e g r e e \displaystyle{ 360 de gr e e } 360 d e g ree 2 π r a d i a n s \displaystyle{ 2 \pi ra dia n s } 2 π r a d ian s
sin ( θ ) = sin ( x ) = sin ( x + 2 π k ) sin ( θ ) = sin ( π − x ) = sin ( π − x + 2 π k ) \begin{align*}
\sin(\theta) & =\sin(x)\\
& =\sin(x+2\pi k)\\
\sin(\theta) & =\sin(\pi-x)\\
& =\sin(\pi-x+2\pi k)
\end{align*}
sin ( θ ) sin ( θ ) = sin ( x ) = sin ( x + 2 πk ) = sin ( π − x ) = sin ( π − x + 2 πk )
θ = x + 2 π k \theta = x + 2\pi k θ = x + 2 πk θ = π − x + 2 π k \theta = \pi - x + 2\pi k θ = π − x + 2 πk
Persamaan Cosinus
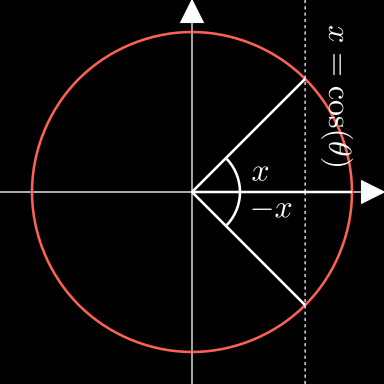
cos ( θ ) = cos ( x ) = cos ( x + 2 π k ) cos ( θ ) = cos ( 2 π − x ) = cos ( 2 π − x + 2 π k ) = cos ( − x + 2 π k ) cos ( 2 π − x ) = cos ( − x ) = cos ( x ) \begin{align*}
\cos(\theta) & =\cos(x)\\
& =\cos(x+2\pi k)\\
\cos(\theta) & =\cos(2\pi-x)\\
& =\cos(2\pi-x+2\pi k)\\
& =\cos(-x+2\pi k)\\
\cos(2\pi-x) & =\cos(-x)=\cos(x)
\end{align*}
cos ( θ ) cos ( θ ) cos ( 2 π − x ) = cos ( x ) = cos ( x + 2 πk ) = cos ( 2 π − x ) = cos ( 2 π − x + 2 πk ) = cos ( − x + 2 πk ) = cos ( − x ) = cos ( x )
θ = x + 2 π k \theta = x + 2\pi k θ = x + 2 πk θ = − x + 2 π k \theta = -x + 2\pi k θ = − x + 2 πk
Digabung: θ = ± x + 2 π k \theta = \pm x + 2\pi k θ = ± x + 2 πk
Persamaan Tangen
tan ( θ ) = tan ( x ) = tan ( x + π k ) θ = x + π k \begin{align*}
\tan(\theta) & =\tan(x)\\
& =\tan(x+\pi k) \\
\theta &= x + \pi k
\end{align*}
tan ( θ ) θ = tan ( x ) = tan ( x + πk ) = x + πk
k k k
Persamaan a cos(x) + b sin(x) = c
Persamaan tersebut mirip dengan:
cos ( x + θ ) = cos ( θ ) cos ( x ) − sin ( x ) sin ( θ ) cos ( x − θ ) = cos ( θ ) cos ( x ) + sin ( θ ) sin ( x ) \begin{align*}
\cos(x+\theta) & =\cos(\theta)\cos(x)-\sin(x)\sin(\theta)\\
\cos(x-\theta) & =\cos(\theta)\cos(x)+\sin(\theta)\sin(x)
\end{align*}
cos ( x + θ ) cos ( x − θ ) = cos ( θ ) cos ( x ) − sin ( x ) sin ( θ ) = cos ( θ ) cos ( x ) + sin ( θ ) sin ( x )
Karena a a a b b b a a a b b b a a a cos ( θ ) \cos(\theta) cos ( θ )
k cos ( θ ) cos ( x ) + k sin ( θ ) sin ( x ) = k cos ( x − θ ) a cos ( x ) + b sin ( x ) = c \begin{array}{cccccl}
k\cos(\theta) & \cos(x) & + & k\sin(\theta) & \sin(x) & =k\cos(x-\theta)\\
a & \cos(x) & + & b & \sin(x) & =c
\end{array}
k cos ( θ ) a cos ( x ) cos ( x ) + + k sin ( θ ) b sin ( x ) sin ( x ) = k cos ( x − θ ) = c
Kita samakan kedua persamaan di atas sehingga kita bisa melakukan pencocokan koefisien.
k cos ( θ ) = a cos ( θ ) = a k k sin ( θ ) = b sin ( θ ) = b k tan ( θ ) = sin ( θ ) cos ( θ ) = b k × k a = b a \begin{align*}
k\cos(\theta) & =a\\
\cos(\theta) & =\frac{a}{k}\\
k\sin(\theta) & =b\\
\sin(\theta) & =\frac{b}{k}\\
\tan(\theta) & =\frac{\sin(\theta)}{\cos(\theta)}\\
& =\frac{b}{k}\times\frac{k}{a}\\
& =\frac{b}{a}
\end{align*}
k cos ( θ ) cos ( θ ) k sin ( θ ) sin ( θ ) tan ( θ ) = a = k a = b = k b = cos ( θ ) sin ( θ ) = k b × a k = a b
Sekarang kita mencari nilai k k k
k cos ( θ ) = a kuadratkan k 2 cos 2 ( θ ) = a 2 k sin ( θ ) = b k 2 sin 2 ( θ ) = b 2 + k 2 ( cos 2 ( θ ) + sin 2 ( θ ) ) = a 2 + b 2 k 2 = a 2 + b 2 k = a 2 + b 2 \begin{array}{ll|c|llr}
k\cos(\theta) & =a & \text{kuadratkan} & k^{2}\cos^{2}(\theta) & =a^{2}\\
k\sin(\theta) & =b & & k^{2}\sin^{2}(\theta) & =b^{2} & +\\
\hline & & & k^{2}(\cos^{2}(\theta)+\sin^{2}(\theta)) & =a^{2}+b^{2}\\
& & & k^{2} & =a^{2}+b^{2}\\
& & & k & =\sqrt{a^{2}+b^{2}}
\end{array}
k cos ( θ ) k sin ( θ ) = a = b kuadratkan k 2 cos 2 ( θ ) k 2 sin 2 ( θ ) k 2 ( cos 2 ( θ ) + sin 2 ( θ )) k 2 k = a 2 = b 2 = a 2 + b 2 = a 2 + b 2 = a 2 + b 2 +
Untuk menyelesaikan a cos ( x ) + b sin ( x ) = c a\cos(x) + b\sin(x) = c a cos ( x ) + b sin ( x ) = c k cos ( x − θ ) = c k\cos(x-\theta)=c k cos ( x − θ ) = c k = a 2 + b 2 k=\sqrt{a^2+b^2} k = a 2 + b 2 θ \theta θ cos ( θ ) = a k \cos(\theta) =\dfrac{a}{k} cos ( θ ) = k a sin ( θ ) = b k \sin(\theta) =\dfrac{b}{k} sin ( θ ) = k b tan ( θ ) = b a \tan(\theta) =\dfrac{b}{a} tan ( θ ) = a b θ \theta θ θ \theta θ a a a θ \theta θ b b b c c c θ \theta θ